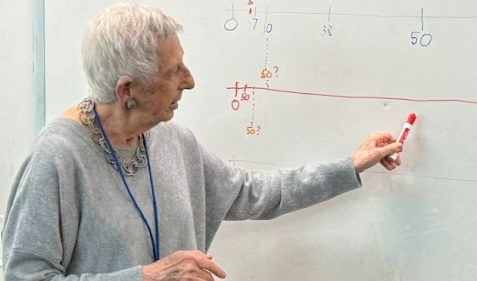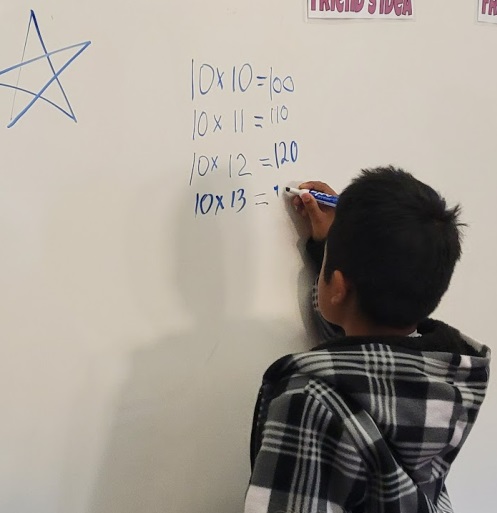fourth grade Archives - MARILYN BURNS MATH

Decimals Fractions General Interest Interviews One-on-One Number and Operations Numerical Reasoning

How Was Amber Reasoning?

The fifth-grade class I’m working with this year is studying addition and subtraction of fractions, and I asked to “borrow” the class to see how they would view Amber’s solution. I describe how I structured the lesson and have also included students’ writing.

Marilyn BurnsDecember 14, 2024

Division

A Lesson Designed Around One Problem—100 ÷ 3

Did I teach an entire division lesson focused on just one problem? Yes! From giving many hundreds of interviews where students solve problems mentally, we’ve learned that solving 100 ÷ 3 is often a challenge. After recently interviewing and hearing two answers for 100 ÷ 3 that I’d never heard before, I taught this lesson.

Marilyn BurnsDecember 9, 2024

Division Word Problems

My First Ever Card Sort . . . And I’ll Do More

Have you ever engaged students with a Card Sort? I’ve known about Card Sorts for quite a while, but this was my first go with it. The students were engaged and the experience was useful for building their understanding of division. For sure, I’ll do more.

Marilyn BurnsDecember 1, 2024

Area and Perimeter General Interest Geometry Measurement

Part 2: Untangling Area and Perimeter

In my previous blog, I described a lesson I taught based on measuring the area and perimeter of my foot. Here I describe what happened when I returned to the class to have the students think more about the data they recorded and the mathematics it revealed.

Marilyn BurnsJune 13, 2024

Area and Perimeter General Interest

Untangling Area and Perimeter

This is a lesson that I’ve taught for many years when teaching about area and perimeter. I recently revised the lesson and I think my changes were an improvement. How did I change the original plan? What was my thinking behind the changes? How did the students respond?

Marilyn BurnsMay 23, 2024

General Interest

Milk Cartons, Origami Paper, a Desmos Tool, and More

After teaching this lesson, I taught it to another class to work out some of the kinks. My, it’s hard and time-consuming to prepare for and plan lessons. I hope my story makes the lesson accessible for other teachers and students to enjoy.

Marilyn BurnsApril 16, 2024

Estimation General Interest Number Lines Numerical Reasoning Problem Solving

Teaching a Number Line Lesson

In my last blog, I describe how I planned a lesson about number lines. In this blog, I describe what actually occurred when I taught the lesson to a class of fourth graders. Read about which parts of my plan I followed, when and why I made some changes, and what the students did on the assignment I gave them.

Marilyn BurnsFebruary 20, 2024

Numerical Reasoning Silent Math

Silent Math

Have you ever used Silent Math with your students? During this instructional routine, no one talks, not even the teacher. Read more to learn about how Silent Math works and why it’s a staple of my instruction.

Marilyn BurnsFebruary 7, 2024

Division General Interest Number and Operations Numerical Reasoning Place Value Problem Solving Real-World Problems Word Problems

Mulling about Teaching Division

Teachers often report that division is hard to teach. How can we help build students’ understanding? Read on for an introductory division lesson I taught to fourth graders.

Marilyn BurnsJanuary 18, 2024

Fractions General Interest Number and Operations Numerical Reasoning

Representing 4/5 and 5/4: A Fraction Lesson

I took the photo of the board at the end of a fraction lesson I taught to fourth graders. The lesson engaged the students with representations of 4/5 and 5/4, using drawings the students had made. Read about how the lesson unfolded and what I learned about the students.

Marilyn BurnsJune 20, 2023

fourth grade Archives - MARILYN BURNS MATH

How Was Amber Reasoning?

A Lesson Designed Around One Problem—100 ÷ 3

My First Ever Card Sort . . . And I’ll Do More

Part 2: Untangling Area and Perimeter

Untangling Area and Perimeter

Milk Cartons, Origami Paper, a Desmos Tool, and More

Teaching a Number Line Lesson

Silent Math

Mulling about Teaching Division

Representing 4/5 and 5/4: A Fraction Lesson

Categories

Subscribe to
Marilyn Burns Math

fourth grade Archives - MARILYN BURNS MATH

Categories

Subscribe to Marilyn Burns Math

Subscribe to
Marilyn Burns Math