When I previously visited this class, I taught a lesson about area and perimeter using the area of my foot that I had traced onto centimeter squared paper and string equal in length to the perimeter of my foot. The students had been fully engaged in the lesson, as they typically are when they have the opportunity for a hands-on experience.
Now I was interested in having the students think about the mathematics related to their experience. I was reaching for what Anne Watson described in her “ThenWhats” article, that a classroom activity “can sometimes go nowhere if we do not think about where to go next.” Here my mathematical goals were for students to think about how rectangles with the same perimeter could have different areas, and that rectangles that were closer to the shape of a square had greater areas than rectangles that were longer and skinnier.
A Reminder About the Activity That Preceded This Lesson
In the previous lesson, I demonstrated for the class how I had estimated the area of my foot, which I had traced on centimeter square paper, to be about 175 square centimeters.
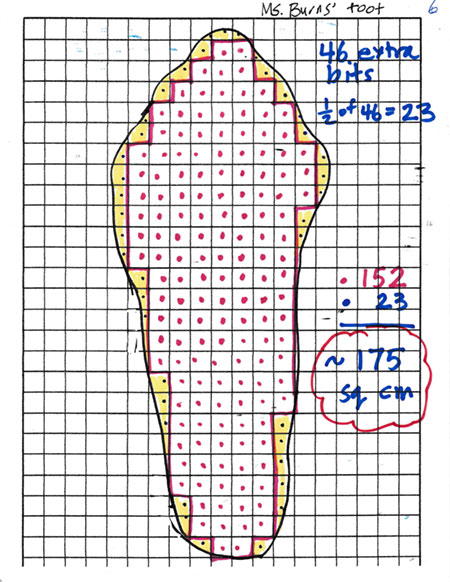
This shows how I estimated the area of my foot.
Next I had placed string around my foot perimeter and measured it to be 60 centimeters. I cut enough 60-centimeter lengths of string so each pair of students had one. Their task was to tape the string into a rectangle on squared centimeter paper, figure its area, and post their data.

Students were engaged in forming rectangles with the string and figuring out their areas.
Returning to the Class to Revisit the Lesson
When I returned to class, I gathered the students on the rug, posted the chart of their data, and began to ease my way into a class discussion. My goals were for students to understand that rectangles with the same perimeter could have different areas, and those that were closer to the shape of a square had greater areas than rectangles that were longer and skinnier.
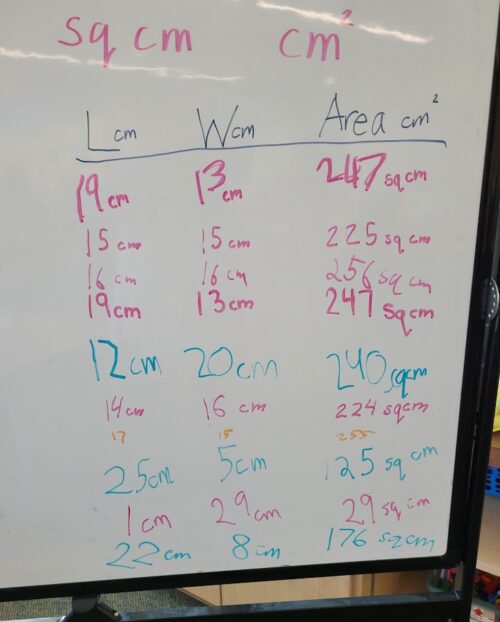
This was the chart they had completed in the previous lesson.
A Reflection on Class Discussions
My goal for a class discussion like this is to help students reflect on the experience, think about the mathematics involved, and stretch their understanding. When I lead class discussions like this, I strive for a balance of guiding the discussion, having students talk and listen to each other, and keeping their focus on moving the conversation toward my mathematical goal. While I’m often tempted to tell students what I’d like them to understand, I’ve shifted over the years to giving students opportunities to make sense for themselves.
Easing Into the Class Discussion
I began by asking students to describe the investigation that produced the chart. I asked, “Suppose a visitor came into the room now who wasn’t here when we created this chart. How would you explain what we were investigating?” This is a low-hanging fruit question that I knew would engage many of them in contributing and I gave all who were willing the chance to share. I wanted to communicate that I wasn’t looking for one right answer but was interested in hearing all of their ideas.
Most of their comments were snippets that told part of the story and were useful for giving other students ideas about what they might contribute.
“You showed us how you figured the area of your foot.”
“You outlined whole squares and colored the rest in yellow.”
“We all had string and could make any rectangle we wanted.”
“The string went around your foot.”
“It was your perimeter.” (Here I interjected, “How long was my perimeter string?” They remembered that it was 60 centimeters.)
“We wrote our measurements on the chart.”
“We got different areas.”
Revisiting the Chart and Reporting What I Noticed
Then I drew their attention to the chart with their measurement data to shift from reporting on what they did to thinking about what the data revealed. I began, “Now I want to tell you some things that I observed when you were making your rectangles and posting on the chart.”
First I told the class that I noticed after Cole and Gemma entered their 15-by-15-centimeter square, the second entry on the chart, that they were confused because its area was so much more than the area of my foot. I asked, “Can you recall what confused you?” Cole answered, “We thought they’d be the same so we thought either yours was wrong or ours was.” Gemma added, “But we checked our multiplication and we were right.” Several other students said that they were also surprised that the areas they were figuring was so much more than mine.
I next told the class that I was confused to see a 15-by-15-centimeter square posted and then a 16-by-16-centimeter square posted underneath. Chatter broke out about measuring not being exact, about it being hard to tape the string exactly on the lines, that the string was sort of stretchy. I asked, “Which of these two squares has a perimeter of 60 centimeters, like my string?” It was easy for them to figure that it was the 15-by-15-centimeter square.
I then told the class that I noticed that some of the other rectangles on the chart also didn’t have perimeters of 60 centimeters. Brooke said, “Yeah, we did the 19-by-13 rectangle, and its perimeter was 64, so it wasn’t right.” David added, “Ours was the 12-by-20 square, and that was 64, too.”
I pointed to the next-to-last entry on the chart, which was a 1-by-29-centimeter rectangle. I asked, “What about this area? How does it compare to the area of my foot?” “That was ours,” Elise said and added, “it has the right perimeter but the area was much, much less.” “Our area was less, too,” Cedric said, referring to the 25-by-5-centimeter rectangle he and his partner had made.
I then asked Asher to recall what he had done before writing the last entry on the chart, a 22-by-8-centimeter rectangle with an area of 176 square centimeters. He explained how he tried to make a rectangle that looked more like a foot and get as close as possible to the area of my foot.
I Recorded on the Board What They Reported
I then made the decision to record their ideas on the board. I had several reasons for doing this. After the discussion, I planned to ask them each to write about their ideas, and recording on the board was a way to model for them what they were to do. Also, I’ve found in general that when I take the time to record students’ ideas, it gives them the opportunity to reflect on each other’s thinking. Also, recording their ideas gave some of them the chance to explain their thinking again. I try and capture students’ comments verbatim.
Some people got different rectangles because of different measuring.
The string has to look like a foot. The closest numbers together have the biggest area. Numbers further apart (like 1 x 29) have small areas.
It has to kind of make a foot shape, not exact but roughly foot-ish. Nothing will be perfect.
If I made a triangle with the same string as a rectangle, the perimeters are the same but the areas would be different.

This shows their chart and my recording of their comments.
The Writing Assignment
I then introduced the writing assignment. I wrote a suggested title on the board: What I Learned about Area and Perimeter. I told them that I was interested in their ideas and that it was OK to refer to the ideas on the board. Here are samples of their work:

When she wrote “numbers that are closer to each other,” this student was referred to the dimensions of the rectangle.

This student used numerical examples to support the idea that with rectangles, different lengths and widths can produce different areas.

Her paper demonstrates her understanding that the same perimeter can produce rectangles with “endless different areas.”
A Reflection about Student Writing
I’m convinced that having students write in math class is valuable for several reasons. It gives me a way to learn more about what individuals understand. Class discussions give me a general sense of where the class is, but individual student writing gives me important information about each student. Also, writing about their thinking gives students the opportunity to reflect on the mathematics in the lesson. Writing isn’t easy for many students. It helps when they first have a chance to voice their ideas. I’ve learned that it also helps when they have some models to follow, like those I had recorded.
Another Then What
To follow up this experience, I gave each student a 5-by-5-centimeter square to cut into several smaller pieces and tape into a new shape. They agreed that all of their shapes would still have the same area of 25 square centimeters. I told them also to cut a length of string equal in length to their shape’s perimeter and tape the string onto their new shape.

Rather than use the information she had figured that the perimeter was equal to 22 cm, this student chose to place string around the shape to measure a length of string equal to its perimeter.

After she cut the perimeter string, she taped it to her shape, as I had instructed.
This experience produced a collection of shapes with the same area but with different perimeters. We taped their shapes into a graph to revisit as another Then What.

This display of the students’ shapes shows that shapes with the same area of 25 centimeters can have different perimeters.

