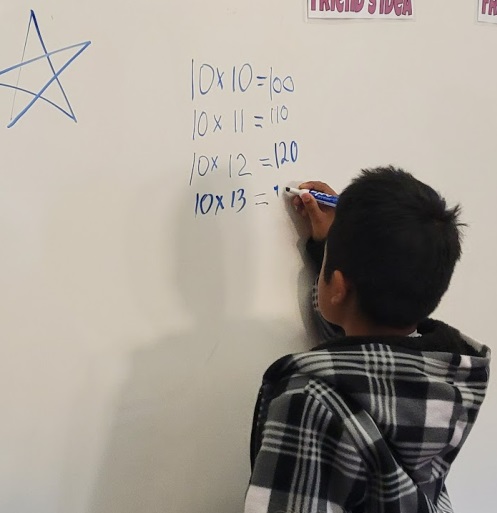Silent Math is a pedagogical routine I’ve used for many years. I can’t remember exactly when I first learned about Silent Math lessons. I think it was when I observed a classroom lesson in the beginning years of my teaching. I don’t remember the teacher or the specific lesson, but I remember being impressed by the students’ engagement and enthusiasm. I’ve used Silent Math from time to time ever since.
How Silent Math Works
The routine is simple: After the teacher draws a star on the board, no one talks. Not even the teacher. And then, when the teacher erases the star, the class discusses what occurred.
The first time I do this with a class, I explain the Silent Math routine. I typically say something like this: We’re going to do math now with no one talking, not even me. It’s called Silent Math. I’ll write a problem on the board. Then I’ll hand the marker to someone to come up (without talking) and write the answer.
Next I explain what the rest of the class does when a classmate writes an answer: After someone has written an answer, show a thumb up if you agree, a thumb down if you disagree, or put your thumb sideways if you’re not sure.
I then introduce the idea of the “silent star.” I explain: When I draw a star on the board, that’s the signal that we’ll all be quiet. When I erase the star, we’ll have a discussion about what happened. (I’ve found that it’s not unusual when I erase the star to hear the class exhale in unison.)
My Recent Use of Silent Math for a Warmup to a Lesson
I recently used Silent Math as a warmup for a lesson on volume with Mariah Murga’s fifth grade class at John Muir Elementary School in San Francisco, CA. For this warmup, I chose problems with numbers that I knew would be useful for estimating during the volume exploration.
I began by asking the students if they had ever heard of Silent Math. Some of them were familiar with the routine from when they were third graders and I asked several to share what they remembered. After their explanations, I drew a star on the board and wrote the first problem: 10 x 10 =. I selected a student who came up to the board and wrote the correct answer. I continued with other problems that had one factor of 10.

For the first string of problems, I used multiplication problems that had one factor of 10.
Multiplying by 10 was easy for the students. Well, actually, the second student made an error, writing 121 for the answer to 10 x 11. (This is an example where a student gave the correct answer to a different question, here the correct answer for 11 x 11.) When he saw the thumbs-down signals, he passed the marker to a classmate who came up and changed the 121 to 110. The boy who made the error didn’t seem disturbed. Mariah has worked hard with the class to build a supportive community of learners. She has helped the students realize that we all make errors and that errors are an opportunity to look at something in a different way. This was wonderful to witness.
After I erased the star, we had a discussion. I asked students to explain how they decided on the products and students explained differently. All of their explanations pointed to their having learned the pattern that multiplying by 10 results in tacking on a zero to the other factor.
I then drew the star on the board again and began another string of problems, this time multiplying three factors, two of which were 10. Since the lesson was going to focus on volume, these problems would provide a reference when I later asked them to estimate the volume of a box by multiplying its three dimensions.
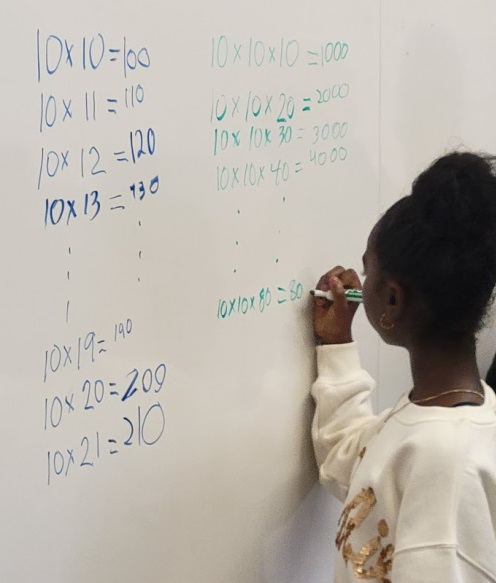
For the second string of problems, I used multiplication problems with three factors, two of which were 10.
As I did with the first string of problems, after I erased the star, we had a discussion about how they thought about figuring out the products. Again, students’ explanations differed. Some first multiplied 10 x 10 and then knew about tacking on two zeros when multiplying the third factor by 100. Some started by multiplying 10 times the third factor (the factor that was different in each problem) and then tacking on one more zero.
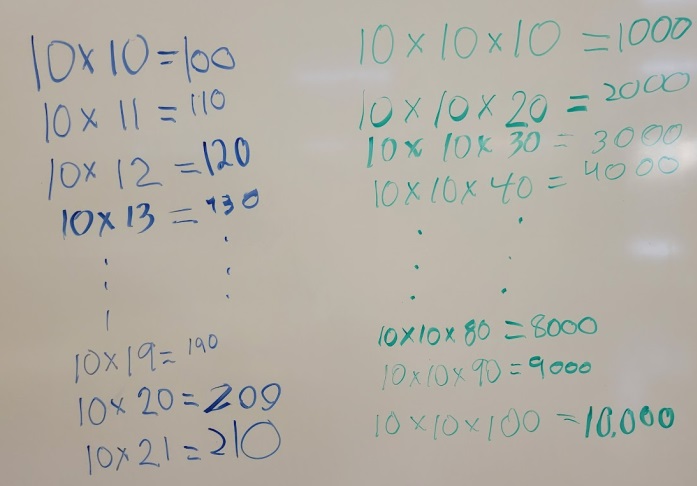
Here are the problems we used for the Silent Math portion of the lesson.
From Silent Math to Volume
If you’re interested in learning about where the lesson shifted from here to a volume exploration, I’m working now on a blot to explain how that unfolded. (Stay tuned.)
Why Do I Use Silent Math?
I’ve found that this silent math routine is useful for encouraging students to focus visually on what’s on the board without the distraction of hearing from others. It eliminates having those who think more quickly blurt out an answer. It’s a change from the “think, pair, share” protocol that I often use and is especially effective when I want to encourage students to look for patterns in a string of problems and make conjectures about the math. Rashida Carter, who also teaches fifth grade at John Muir, observed when I was teaching in Mariah’s class and then taught the lesson to her class. Rashida wrote in a follow-up e-mail to me: They loved silent math! All hands were up, including my newcomers who are predominantly Spanish speaking.
If You’re Interested in More―Including How to Use Silent Math as a Small Group Activity
In a book I wrote with Maryann Wickett, Teaching Arithmetic, Lessons for Extending Multiplication, Grades 4–5, “Silent Multiplication” is the title of Chapter 4. (You can download a PDF of the chapter here.) In this chapter, we describe how we used a series of silent math lessons to help students develop strategies for solving increasingly complex multiplication problems. The lessons focus on having students examine the effects on products when one factor is doubled, when both factors are doubled, when one factor is halved, when one factor is halved while the other is doubled, and more. The chapter includes an extension for using silent math as a small group activity instead of as a class lesson. It also includes examples of the students’ small group work, and samples of reflections written by students about what they learned by playing Silent Multiplication. A Q&A section at the end of the chapter provides help with leading discussions after a silent math experience.