The first time I looked at the video clip of Adrian explaining why 5/6 is greater than 1/4, my reaction was “WHOA!” I was completely baffled by how Adrian reasoned. Here’s what I did to understand Adrian’s thinking and then to prepare for using the video with a class of 4th graders.
Listen to Adrian
A great deal is packed into this 38-second video clip of Adrian figuring out his thinking as he talked.
What I Noticed from Listening to Adrian
Note: This is one of the questions from Listening to Learn, Interview 9, Foundations of Fractions. Here’s what I noticed from watching the video clip:
- Adrian knew without having to figure that 5/6 was greater than 1/4.
- He seemed confident and immediately launched into explaining why.
- Adrian worked hard to explain his reasoning . . . really hard.
- Even when he self-corrected and back-pedaled, Adrian seemed confident and kept his focus.
- Adrian relied on converting to common denominators, but in a unique way.
- Amy was a neutral listener, giving Adrian time and space to work through his thinking.
While Adrian’s explanation was a wonderful opportunity to delve into his thinking process, I was flummoxed and had to watch this video clip many times in order to make sense of how he was reasoning. As I rewatched, I paused the video multiple times to parse and record what he said. Only then did I figure out how Adrian made sense of the problem.
Along with being a digital interview assessment tool, Listening to Learn includes a collection of professional learning interactive Labs. More than 40 Labs are currently on the tool with more slated to be uploaded. One of the Labs focuses on this question of comparing 5/6 and 1/4 and includes video clips of seven students, each with reflections on how they reasoned. Here’s a screen shot from that Lab with the reflection on how Adrian reasoned:

Using Listening to Learn Videos for Class Instruction
I’m interested in using video clips from Listening to Learn math interviews in classroom lessons. (I’ve written several other blogs about my experiences doing this.) I recently met with the three 4th grade teachers at a nearby school in Mill Valley, CA, and asked to “borrow” a class. They agreed and asked to observe a lesson about fractions. I talked with them about my teaching idea for engaging the students with comparing fractions and also with Practice Standard 3: Construct viable arguments and critique the reasoning of others.

As students explained their reasoning, I recorded their ideas on the board. This provided a reference for them to compare what they watched on the videos with their own idea.
My Lesson Plan for Using the Video of Adrian
Here’s the lesson plan I presented to the teachers for using the video of Adrian with their students.
- Write the problem on the board: Which is greater—1/4 or 5/6?
- Have students talk with a partner and then share their ideas (think, pair, share).
- Record the students’ ideas on the board. (This gives them experience with the first part of the math practice standard 3: Construct viable arguments.)
- Show video clips of students other than Adrian explaining why 5/6 is greater. Show each clip twice. For each, have them decide if the student’s reasoning matched one of their ideas. (This gives them experience with the second part of the practice standard: critique the reasoning of others.)
- After watching the video clip of Adrian twice, show it again and this time pause the video after each of Adrian’s statements to have students make sense of his reasoning.
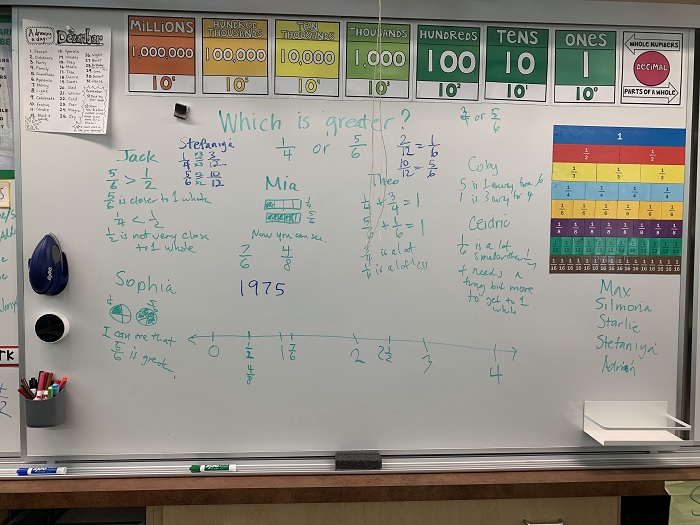
Here’s what the whiteboard looked like after the students presented their ideas (step 3). At the lower right of the whiteboard, I listed the students they would watch comparing 5/6 and 1/4.
The students seemed intrigued as they watched the videos of students reasoning. They were able to connect what they saw with explanations that I had written on the board. None of them had reasoned the way Stefaniya did or the way Adrian did, and these discussions were especially lively and interesting.
My Takeaway from This Experience
It’s hard to follow someone else’s reasoning. I was reminded of that as I listened, over and over, to Adrian explain in the video clip. Too often in my early years of teaching, I worked hard to prepare explanations for my lessons that I thought would help students understand. I came to realize that I was doing the bulk of the work and, over time, shifted my practice to give students more opportunities to reason and explain their reasoning. I learned to listen more to students and draw on their ideas to help nudge, nurture, and extend their learning. In this lesson, asking students to analyze the students’ explanation on video served to engage them in the work of making sense. The students were interested and engaged.
If you try this lesson in your class, I’d love to hear your feedback.
Marilyn

