This lesson is a hands-on exploration that connects the two ideas of area and perimeter and, I think, helps students build understanding of both. The lesson is based on one I wrote about in my very first Math Solutions professional book―A Collection of Math Lessons From Grades 3 Through 6. (You can download the chapter, “Foot Activities,” where I describe the entire unit.) Since then, I’ve included this introductory lesson in all four editions of About Teaching Mathematics. It’s a keeper. But most recently, I revised the original lesson and taught it to a fourth-grade class. Here I describe what I did, what my thinking was behind the changes I made, and what happened in the class.
A Look Back at My Original Plan
I’ve typically begun the unit by asking students to trace one of their feet on squared centimeter paper and figure its area. Students would then cut a piece of string or yarn equal in length to the perimeter of their foot, tape their foot string on the squared centimeter paper to make a square, and compare the areas of their feet and the square. Here’s an example of how a student did this when I first wrote about the lesson. The discrepancy between the two area measures always results in a lively discussion.
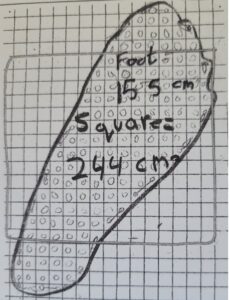
This student was surprised that the areas of her foot and square were so different even though they had the same perimeters.
How I Changed My Plan
Before I taught this lesson to Amie Levin’s fourth grade class, she had the students trace their feet and cut yarn equal to their perimeters. She didn’t ask them to figure the area of their feet or explore another shape with the perimeter string—that was what I planned to do.
But, before going to class, I changed my plan. I decided that instead of giving students the challenge of figuring out the areas of their feet, I would show them how I figured the area of my traced foot.
I projected six images, one at a time, and explained the process that I used to determine that the area of my foot was about 175 square centimeters. [Note: I’ve attached a PDF of these six images, Ms. Burns’ Foot, in case you want to use them with your class.]
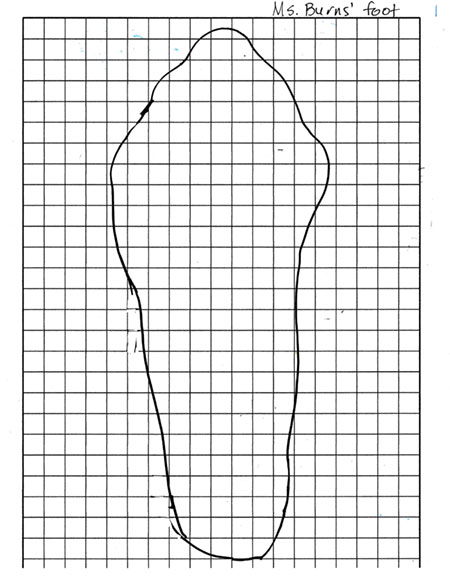
Image 1: I showed the students my foot traced on squared centimeter paper, as they had done, and asked, “What do you think I’m going to do next?” Several students shared ideas. “Figure the area.” “Make a graph.” “Count the squares inside.” I then told them that I was going to figure out the area of my foot so I knew how many square centimeters were inside the outline.
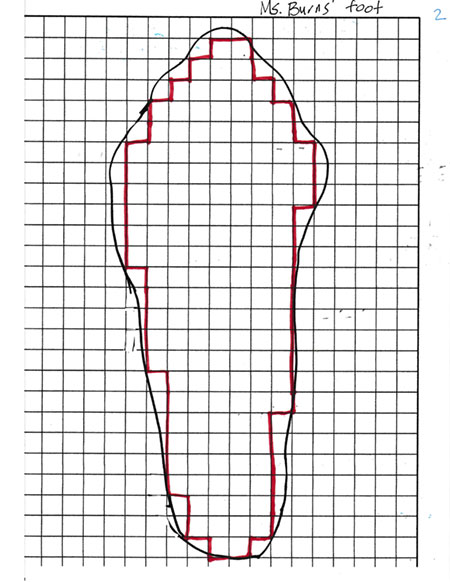
Image 2: Next I showed them how I outlined all of the whole squares inside my foot and asked them what they thought I did next. Two students had ideas. “You counted them.” “You divided it up into rectangles.”
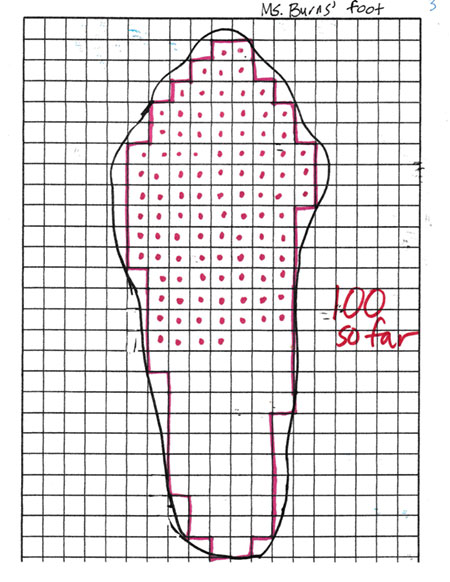
Image 3: I then displayed what I actually did and explained that I counted the whole squares, marking each as I counted. I stopped after I had reached 100 square centimeters and asked, “How many whole squares do you estimate there were after I counted them all?” They had different ideas but all estimates were 150 or more square centimeters.
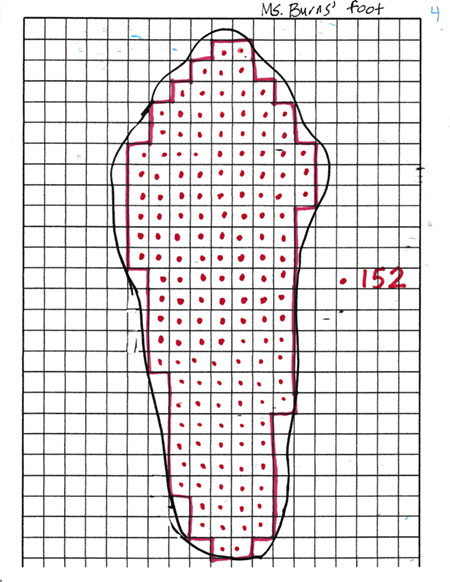
Image 4: The next image showed how I had continued making dots in squares and found that there were 152 whole squares in my foot outline.
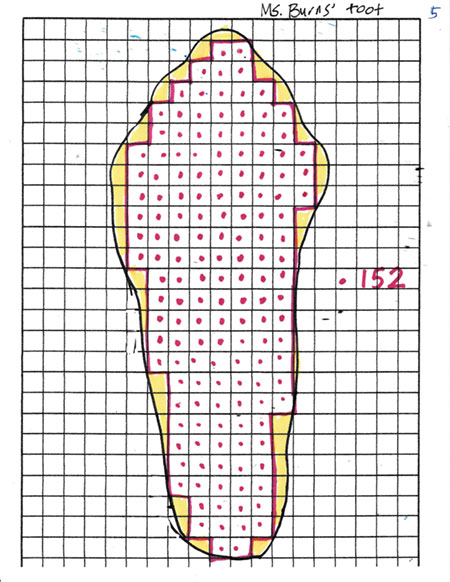
Image 5: I explained, “This shows how next I highlighted in yellow the extra bits that were inside my foot but outside the whole squares.” We talked about what to do with these. Some students noticed that some of the bits were about half a square and said we could count the halves and combine them. Some said we could combine big pieces and little slivers.
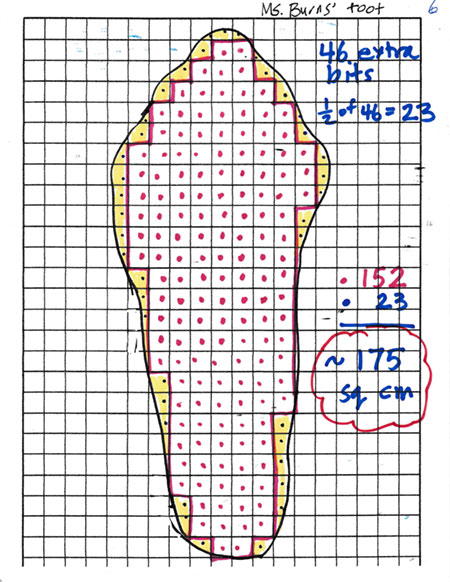
Image 6: I projected my last image, telling them that what I decided to do was to count all of the extra bits and take half, figuring that was a reasonable way to estimate. I counted 46 extra bits, divided by 2, and added 152 plus 23. I concluded, “The total area of my foot is about 175 square centimeters.”
Ah, so many reasons impact our teaching decisions. When giving students problems to tackle, I mull over how much help to give them ahead of time by scaffolding or explaining. So, why did I change my plan this time and instead of asking students to figure their own foot areas, show them how I figured the area of my foot? Even to me, it felt different from what I typically do and recommend.Here’s how my thinking evolved. I revisited my math goal for the lesson, which was to give students experience with area and perimeter in a way that engaged them with the idea that shapes that have the same perimeter do not necessarily have the same area. From my own previous teaching experiences with this lesson, I knew that measuring the area of their own foot and then the area of a square with the same perimeter typically results in them being surprised, confused, and curious. The experience produces what I think is the essence of a valuable teaching moment, when students reach an impasse in their thinking and understanding. Then I have the teaching challenge of helping them confront their mathematical confusion in a way that can lead them to further sense making.
My decision to use my foot instead of students each using their own evolved from a conversation with Jenna Laib, who was revisiting my original lesson with me. Jenna’s suggestion was that if the students all worked with the same foot (mine) and explored different rectangles from my perimeter string, then we could look at more data about the same foot. They’d still reach the same impasse and have the same follow-up teaching opportunity.
After talking with Jenna, I argued with myself and went back and forth. Don’t I want students to grapple with problems for themselves? Why was I “robbing” them of the opportunity to decide how to figure out their foot area? But I kept my mathematical goal in mind and decided that the problem I wanted them to engage with is why shapes made with the same perimeter string did not necessarily have the same areas. If they all made different shapes with my perimeter string, the class would have more apples-to-apples evidence to consider.
Also, my revised plan still gave them hands-on experience as they worked in pairs to fashion my perimeter string into a rectangle. Even better, working with a partner would give them the opportunity to collaborate with a classmate instead of working independently on their own foot areas. Was my decision the best one? I’m not sure there’s ever a best teaching decision, but I’m pleased with this choice. Read on.
Next, a Discussion About Area of Rectangles
After figuring the area of my foot, I told the students that I was convinced that 175 square centimeters was a reasonable estimate of my foot area. They nodded in agreement. I also shared that I thought figuring out my foot area had been complicated and kind of tedious. I asked, “Suppose I hadn’t given myself the problem of figuring the area of my foot but instead I had just drawn a rectangle on the centimeter squared paper and figured its area. Why do I think it would be easier to figure the area of a rectangle?” They shared their thinking about how it wouldn’t involve all of those fractional parts, that it would be easier to determine the number of squares inside a square or rectangle, that you could count, or you could just multiply. I modeled drawing a few rectangles on a squared grid on the board and had them figure their areas by counting and also by multiplying the lengths of their sides, something they had previous experience with.
Presenting Their Task
Next, I showed the class my perimeter string and demonstrated for the class how I had placed it on the outline of my foot. I used a meter stick to measure the string so they could see that it was 60 centimeters long. (That length turned out to be really convenient for the lesson, as you’ll read about.)
I showed them the handful of other pieces of string that I had also cut, each equal to my foot perimeter so that pairs of students could each have a 60-centimeter length. I explained their task, “Tape my perimeter string into a rectangle on a piece of squared centimeter paper and figure out its area.” I added, “It’s OK to make a square since a square is also a rectangle, so that would be fine.”
They watched as I set up a chart on the white board with three columns for them to record the length, width, and area of their rectangle. I had a few of the students repeat the directions, and when I felt confident that the students (or most) understood what they were to do, I asked them to get to work.

Students formed rectangles with the perimeter string.
Interrupting Them After Some Data Was on the Board
There was much chatter as they worked and negotiated sharing the two tape dispensers in the class. Figuring out the areas of their rectangles gave students practice multiplying two-digit numbers, which they had recently learned about.
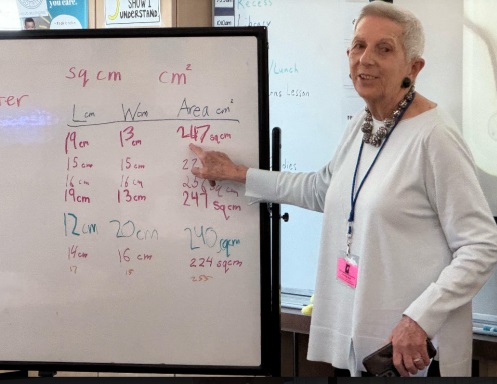
After seven pairs of students had posted their data, I noticed that the dimensions of most of their rectangles didn’t add to 60 centimeters.
I interrupted them to lead a discussion about what I had noticed about their data so far. When I had the students’ attention, I drew a square on the board and asked, “How long should each side of this square be if the perimeter is 60 centimeters, the length of my foot string?” I gave them a few moments to turn and talk with their partners. They agreed that the sides of the square needed to be 15. They explained in different ways. “If you add 15 and 15 you get 30, and that’s half.” “Fifteen times 4 is 60.” “If you cut 60 in half, you get 30, and then you have to cut that in half to get 15.”
I pointed to the second and third entries on the chart, one underneath the other, where one pair had recorded a 15-by-15-centimeter square and the second pair had recorded a 16-by-16-centimeter square. We talked about measurement never being exact, that the perimeter strings I had cut might have been a little different, and also that the string was a little stretchy. Then we investigated the other chart entries and agreed that the 14-by-16-centimeter rectangle was the only other one that had a perimeter of 60 centimeters.
The students went back to work.
Reflection #2
I offer two reflections here. My first is about interrupting the students when they are working. I think that it’s often a useful teaching move to interrupt a class for a check-in, especially after the students have had some time to tinker but haven’t yet come to resolution. Students sharing ideas and raising questions can be useful, as you’ll read about below.
My second reflection is more of a wondering: Should I have anticipated that students wouldn’t use the information that the perimeter was 60 centimeters when taping their strings on centimeter squared paper? Should I have avoided this by telling them to check the measurement of their dimensions to be sure they added to 60 centimeters? After thinking more, I decided that the messiness of measurement was a valuable mathematical reality to experience. Also, I liked them having the experience of adjusting their thinking after considering new information. Teaching calls for making so many decisions, and there’s often more than one productive path.
What Happened After Students Returned to Work
Students went back to work in different ways. Some returned to working with their string, reshaping or correcting to get to 60 centimeters. Some started to explore new shapes with the string. A few abandoned the string and began thinking numerically about shapes with perimeters of 60-centimeters.
One pair was amazed when they made a 1-by-29-centimeter square and learned that its area was so small compared to my foot area. Another pair made a 25-by-5-centimeter square and found that its area was less than the area of my foot. Asher, who had abandoned his partner and was working intensely by himself, head down, thrust his arms in the air and shouted, “I found it!” This was just as the class was leaving for lunch and I talked with him. He had figured that the area of a 22-by-8-centimeter square, which had a perimeter of 60 centimeters, was 176 square centimeters. He said, “It’s soooo close, and I don’t think I can get any closer.” He recorded his data and raced out to lunch.
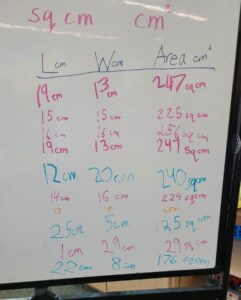
This is the data at the end of class, before the students left for lunch.
Not all learning happens within the tidy confines of one class period. In my earlier years of teaching, I’d try to have some closure at the end of class to summarize the students’ experience and reach a mathematical conclusion. I no longer do that, for two reasons. One is that I found that I was too often barreling to a mathematical conclusion prematurely, focusing on “finishing” my lesson instead of on the students’ thinking. Also, giving time allows the experience to settle and gives students time to reflect on it. Returning to the math on a different day allows me to revisit the mathematics for a fresh look.
Then What?
My experience reminded me of “ThenWhats,” an article written by Anne Watson for the UK Association of Teachers of Mathematics. She wrote the article to “show how some strategies designed to stimulate mathematical learning and thinking can sometimes go nowhere if we do not think about where to go next, or how to use what happens as a result of the strategy.” She also wrote, “The existence of a thenwhat marks an opportunity to change gear.”
I think that the students’ experience in this lesson was mathematically valuable, potentially, but we weren’t at all finished with this idea that a perimeter can produce shapes with different areas. I had involved the students in “doing” and now I also wanted to involve them in “thinking.”
Also, we hadn’t even touched on the idea that shapes with the same area can have different perimeters. I planned a thenwhat and returned to class. You’ll have the chance to read about that in my next blog, Part 2: Untangling Area and Perimeter. Stay tuned.


Marilyn,
What a fine activity to read about!
Using your foot as the model seemed to make the “search” easier for the students to discuss.
Thanks for making my morning so interesting)
Being able to use large print makes it possible for me to follow your thoughts. Great problem that the students enjoyed… then off to lunch!!
Enjoy the beautiful week-end.
Hello to Jeff..
Gratefully, Shirley
How nice to see your messages and glad that I brought a little math into your morning. Regards from Jeffrey and me.