Mulling about Teaching Division

I’m in the weeds mulling about teaching division. When introducing division, what’s the role of contextual problems? Should we start with interpreting division as sharing or grouping? Is it better to introduce problems without remainders first or with and without remainders together? How do I make the connection to multiplication clear and useful?

I’ve been thinking about these questions for a while. And by “for a while,” I’m talking years.

I find mulling with others useful. That’s what I did for this lesson. Jenna Laib is a K–8 math specialist in Brookline, Massachusetts, and she and I talk regularly to share ideas. (If you haven’t read Jenna’s blog posts, you’re in for an educational treat.) Recently, she and I talked about introducing division to fourth graders and we planned a lesson together. We were hoping to encourage students to think about and understand multiplication and division as inverse operations and we decided that a grouping contextual problem would be an effective way to begin.

Jenna first taught the lesson in a class in her school.  Then, after talking together and poring over her students’ work, I taught a close version of the lesson to fourth graders in Aimee Levin’s class at Edna Maguire School in Mill Valley, CA.  I give a step-by-step description below.

We’d both love to hear your feedback.

Introducing the Lesson
I projected this problem and read it aloud.

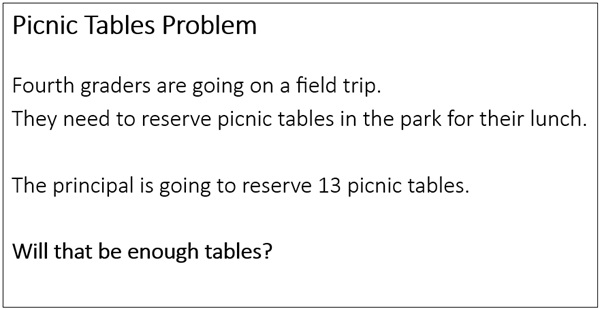
As soon as I finished reading, students’ hands shot up and several offered comments about answering the question. “There isn’t enough information.” “You can’t tell.” “We need to know how many kids there are.” I asked them to turn and talk with their neighbor about what information they needed in order to answer the question. After a few moments, I interrupted them and recorded on the board the two ideas they offered.

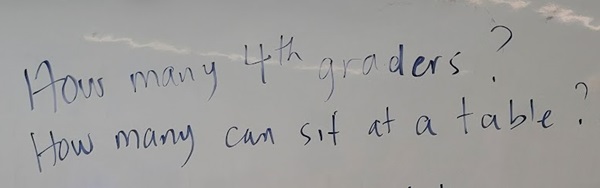
Presenting the Problem
I then projected the problem in a version that included the information they needed to solve it.

I had prepared a sheet for each student with the problem at the top and space for them to show their work. I did this because their teacher, Aimee, had suggested that it was easier for some of them when they had the problem in front of them instead of having to read it from the board.

For Those Who Worked More Quickly
I told them that when they thought they were finished to raise a hand so I could see what they had done. After they began to work, I circulated to get a sense of how they were doing with the problem. I answered questions, reviewed their work, and gave suggestions for their explanations. I noticed that most students concluded 13 tables wouldn’t be enough and that the principal needed to reserve 14 tables. I interrupted the class before all had the chance to finish. (Note: For student who completed the work more quickly, I had a sheet ready with a challenge problem. Thanks to Jessica Goree for this Open Middle problem.)

A Class Discussion
For the class discussion, I wanted to start by hearing their ideas and work toward my goal of talking about multiplication and division as inverse operations. One of my goals was to help them see how they could use what they knew about multiplication to solve division problems.

To begin the discussion, I told the class that I noticed that students had described their reasoning in different ways―writing different math equations and drawing different representations. I decided, because the time I had with them was limited, that I wouldn’t flesh out their ideas. Instead, I told them that I was going to show them the work from a student in another class, also a fourth grader. (Jenna had sent me the work from the fourth graders she taught.) I told them, “I saw some things on your papers that are similar to what students in Massachusetts did and some things that are different.”

Looking at a Student’s Paper
I projected a student’s paper and asked them to turn and talk to their neighbor to see if they could make sense about what this student had been thinking. I told them to be sure to talk with their partner about the equations she included and the drawing she made.

After a few minutes, I interrupted them to hear their ideas. They commented on a variety of things. Here’s some of what they said:
“She wrote three different equations.”
“She drew squares that are tables and she drew more than she needed.”
“She wrote 4s in the squares and I drew dots instead.”
“She used multiplication and division and subtraction.”
“She drew around the 14 tables they needed.”

I asked them how the equations she wrote related to the problem. They identified what the specific numbers meant: 13 was the number of tables the principal ordered, 4 was how many people could sit at each table, 56 was the number of fourth graders, 52 was how many students fit at 13 tables. One boy claimed that she didn’t need to write three equations, that 56 ÷ 4 = 14 was the only equation needed. He said, “The other two were OK but only for support.”

Moving Toward Representing the Problem
I then asked the class a question, “Is this a multiplication problem or a division problem?” Students had different ideas and one commented that multiplication and division were sort of the same and sort of opposites. I wrote “opposite” on the board and took the opportunity to introduce the word “inverse” and explain that multiplication and division are inverse operations. I also reviewed the vocabulary of “product” and “factor.” I find it effective to introduce and reinforce math vocabulary as it arises in the context of lessons.

Next, I asked them to imagine that we had a school newspaper and wrote an article about the field trip that needed a headline. I also told them I’d like the headline to be a math problem that would be helpful for answering the question: Did the principal reserve enough tables? I had them turn and talk with a neighbor. As they reported the numerical problems they’d use for the title of the article, I recorded them.

56 ÷ 4 =

56 ÷ 13 =

56 ÷ 13 =

13 x 4 =

I wrote the problems in the upper left corner of the board. Notice that the second problem, 56 ÷ 13, is crossed out. That’s because the student who had suggested it changed his mind. He explained, “That would give a remainder and it doesn’t make sense.”

My Last Comment to the Class
I thanked them for their thinking and work and ended the lesson by giving them a math suggestion. I told them that when I learn something new in math, I always try and connect it to something that I know and can rely on. And since multiplication is something that I learned before division, it’s easier for me, so I often rely on multiplication to solve division problems.

A Reminder Why Answers Alone Are Not Sufficient
Below is a paper from one of the fourth graders in Aimee’s class. This student answered correctly―and emphatically: There will not! If the answer was all she needed to submit, I wouldn’t have any insights into her thinking. I’ve discussed this paper with several colleagues. (As I wrote earlier, mulling with others is always useful.) What’s important to me is to look at student work to learn what students do understand so that I have a place to start when thinking about how to expand their understanding. You might try that with this piece of work.

A Follow-Up Problem
The next week, Aimee gave the problem below to the fourth graders to see how they’d do with greater numbers. (The problem might also be appropriate for fifth graders.) We chose 234 for the number of students since we thought that 40 x 6 would be accessible to them. This was the case for many and was their starting point. What I hadn’t thought through was my rewording of the question from Will there be enough tables? to Is that the right number of tables? This resulted in some students answering No and writing a version of this explanation: No. He doesn’t need that many. You need 39. However, others answered Yes and wrote a version of this explanation: Yes! There are enough tables, in fact there are actually enough for six more. Both answers are correct!

What About Trying the Problem with Third Graders?
As an introductory division experience, the problem below might work for third graders. I haven’t tried it yet. I think that tables for 4 still makes sense, but I changed the number of students to 28, a multiple of 4 that might not be familiar to the students.

And Back to the Problem for Early Finishers
A suggestion: You might give the Closest Product to 500 investigation to all of your students and see how they approach solving it.

Thanks to Jenna Laib and Lynne Zolli, two people I mull with regularly, for their feedback on this blog before I posted. Thanks to Aimee Levin for allowing me to “borrow” her class.

As always, I’m interested in your feedback and ideas.