The photo below shows the board at the end of the fraction lesson I taught. Well, not exactly at the end of the lesson, but just before I gave the students an assignment so that I could get feedback about their thinking as a result of the lesson. More about that later. As with many lessons, there was much to think about.

Before the Lesson
A few days before, the students completed an assignment that served as a pre-assessment for the lesson. I asked them to draw and label representations of two fractions―4/5 and 5/4. Here are a few samples of their work.

This student used a rectangular representation for 4/5 and then switched to a circle for 5/4.
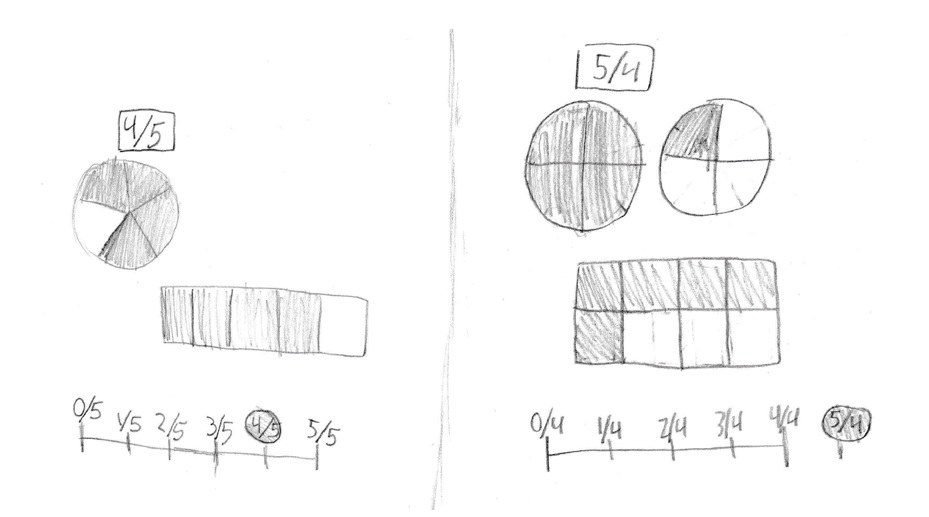
This student drew three representations for each fraction.
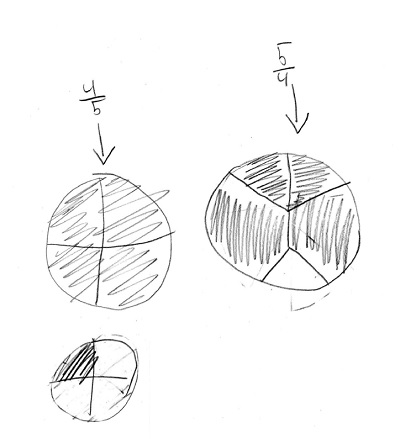
A pre-assessment, as this assignment was, can reveal a student’s confusion. I didn’t use students’ names when I shared their representations with the class.
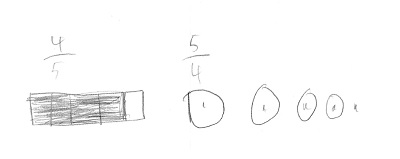
This student’s representation of 5/4 resulted in a lively class discussion.
This student’s representation of 5/4 resulted in another lively class discussion.
To prepare for the lesson, I replicated many of the students’ drawings on the 4-by-6-inch cards you see posted on the whiteboard in the photo above. When I drew these reproductions, I didn’t include the students’ names or the fractions they had written to identify whether the drawing was a representation of 4/5 or 5/4. I also included two cards with shapes that they hadn’t drawn but that had been drawn by fourth graders in a different class when I had taught a related lesson. (You can read about that lesson here.)
How I Began the Lesson
For a warmup, before I showed any of the cards I had prepared, I asked the students to think of a sentence that describes something they know about fractions. After they shared with a partner, I had all who wanted report. Since this wasn’t my class, but one that I was “borrowing” for the lesson, I wanted to know a bit more about the students. One student said, “In fractions, the pieces all have to be equal.” Several other students expressed the same idea in different ways and the idea was especially useful later in the lesson. (A thought: Since I only had an hour for the lesson, I didn’t take the time to record the students’ ideas. I think that would have been useful to do on chart paper so that after this and subsequent lessons, students might both revisit their ideas, and revise their statements, and also add new ideas to the chart.)
Introducing the Cards
On the board, I wrote 4/5, 5/4 and ?? to organize the board into three areas. I showed the deck of cards and explained, “On each card, I reproduced one of the drawings you made, but I didn’t include which fraction it represented.” I told them that together we’d decide in which column I should post each card. For the first few cards, students were reticent and only a few volunteered, but their participation increased as the lesson went on.

For some cards, I’d have students turn and talk before asking someone to share. At times I gave suggestions about language to introduce or reinforce terminology in the context of the exploration. I encouraged the use of “numerator’ and “denominator” to encourage them to become more comfortable using these terms. Also, when a student expressed an idea about a card, I encouraged them to comment on each other’s ideas and referred to the chart posted that they used for book discussions, suggesting that the conversation starters work for math discussions, too.

Notice on the whiteboard at the beginning of the blog that I had also written “ambiguous” on the left side. I hadn’t planned this ahead of time, but its usefulness emerged when students made arguments for how a drawing could represent either 4/5 or 5/4. Three cards eventually wound up in the “ambiguous” column.

Also notice in the “??” column that we decided that two of the representations showed 7/8, which wasn’t one of the fractions we were discussing. In the bottom representation, I followed a student’s lead when she suggested drawing additional vertical lines so that the eighths became evident. (The original drawing had the rectangle divided into four parts, not eight.)

Even though we weren’t discussing 7/8, students thought it was the correct fraction for two of the drawings.
Takeaway #1
I think it was effective to use the students’ work for the representations on the cards. Because the drawings I used for the lesson didn’t come from my ideas or ideas from a textbook, they helped make the students “producers” as well as “consumers” of their learning. I think this was powerful for acknowledging their thinking and engaging them in the lesson. Some squealed their pleasure when they recognized a card that showed a drawing they had done. Some noticed that several had made similar drawings.
After Sorting the Cards
After I had posted all of the cards, I posed a question: Of the two fractions, 4/5 and 5/4, which is closer to 1? Students’ responses were divided among three opinions―that 4/5 was closer, that 5/4 was closer, and that they were both the same distance from 1. It resulted in a lively discussion that was “messy” in that there was lots of confusion and partial understanding, sort of intellectual dissonance. I’m comfortable with this, something I’ve actually become more comfortable with over my years of teaching. What I liked about the discussion is that the focus was on the students’ thinking, on them expressing their ideas, not on my giving an explanation. I tried to remain neutral when listening to their ideas, to learn about their strengths and areas of fragility.
Takeaway #2
The students’ teacher, Jessica, wrote to me after the lesson: It’s so rare to have the time to go that deep and hear so many varied responses to a singular question! I realize that as teachers we are often overwhelmed with all we feel we need to teach and often feel that we don’t have the luxury of giving students time to grapple. But I think that giving opportunities for students to grapple is essential. It keeps the emphasis on the students doing the work of learning, of trying to make sense, of building on their previous understanding and on their classmates’ ideas. This shifts my role from being the chief explainer in the class to having the students be explainers as well, then to listen to their explanations and guide their thinking based on their ideas. It’s tough, I know, but I’m convinced it’s a more effective teaching strategy, especially when we’re pushing students to make sense and create their own understanding. Learning and teaching are complicated.
At the End of the Lesson
To conclude the lesson, I gave an assignment similar to the original assessment, to draw representations of two other fractions―3/4 and 4/3. I also asked them to decide which of those fractions was closer to 1. They worked individually and brought their papers up to me for feedback when they thought they were done or were stuck. I’d give feedback, often asking them to add more, revise, redraw, whatever was needed. Their papers reveal both understanding and struggle.
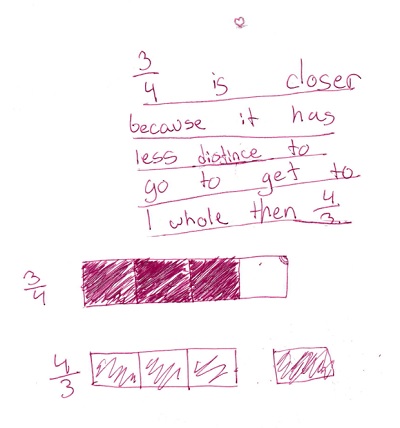
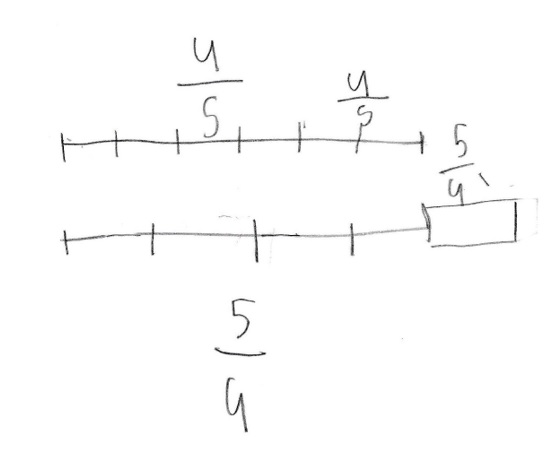
This student thought about the distance of each fraction to 1.
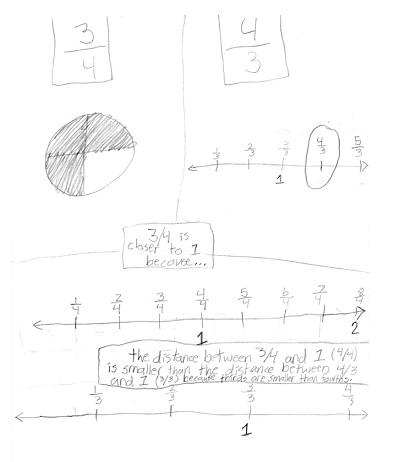
This student relied on number lines to explain.
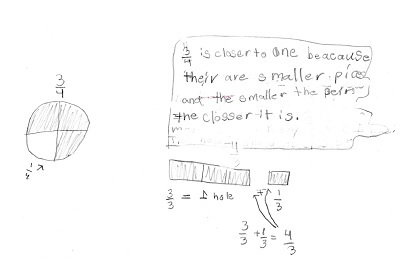
This student knew that 3/4 is 1/4 away from 1 and 4/3 is 1/3 away from 1, and used the idea that 1/3 is greater than 1/4.
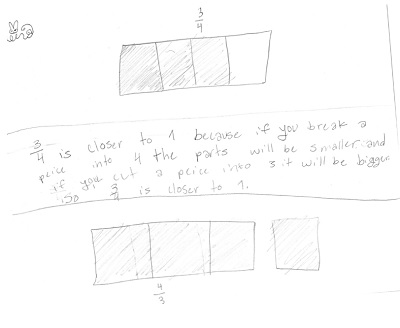
Rectangular representations helped this student explain her reasoning.
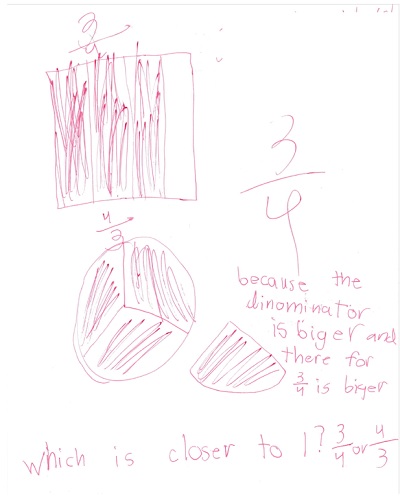
This student explained how the denominators of 3/4 and 4/3 helped with deciding which was closer to 1.
A Final Thought
I’ve been thinking for many years about how to help students develop understanding of fractions. I’m committed to using fraction kits, a length model for thinking about fractional parts that I think is extremely useful . Fraction kits give students concrete ways to explore fractions that I can segue into thinking about number lines, which helps connect fractions to numbers. I wrote about making this transition in this blog.
