Does every experience in life trigger a math experience? Sometimes it seems so.
It did recently when a package arrived with a gift I had ordered for a friend’s birthday. It’s a cordless lamp. I have one that sits on our kitchen table and I love it. You tap the top and the light goes on. Tap again and it gets brighter. And tap once more for its brightest setting. When the light starts dimming, I just plug in the charge cord and connect to a charger. It’s terrific.
About My Cordless Lamp
I bought our cordless lamp after seeing a similar one at our next-door neighbor’s house. I did a search online, found lots of options, and selected one that I liked. I chose vintage copper from the eleven different finishes and bought it. Here’s what arrived.

We liked it so much that we bought two more to give to friends as gifts. Ours had arrived in a long skinny box, and two arrived in a double box like this.

My Recent Experience Ordering a Lamp
Last week, I ordered one for a friend’s birthday gift. A single lamp this time. It arrived in a long skinny outer cardboard box, but when I opened it, I was surprised. Whoa. The box with the lamp was more like a cube, not at all in the shape of a tall, thin lamp.

My first reaction was that I had been sent the wrong item. Clearly this lamp was too short and wasn’t what I had ordered. Not so. I opened the box to investigate (carefully, since it’s for a gift) and learned that they’d changed how they manufacture the stem. Now it’s in two pieces that screw together. OK, no big deal. But why did they do that?
My Mind Turned to Math
I have a friend who works for a company that sells shipping space in container ships, and I learned from him that what’s important when shipping isn’t the weight of the object but the space it takes up in the container. Its volume is what counts. So, I measured the three dimensions of the one-pack and then of the two-pack to compare their volumes.
One-pack box: 7 inches by just under 5 inches by 5 ¾ inches
Two-pack box: 8 ¼ inches by 4 ¼ inches by 14 ½ inches
Then I multiplied the dimensions (converting to decimals and rounding just a bit) to figure their volumes.
One-pack box: 201 cubic inches
Two-pack box: 508 cubic inches
That means that two of the squat one-pack boxes would take up less space that one of the two-pack boxes―402 cubic inches compared to 508 cubic inches. That’s a space saving, maybe even a significant one.
So, if they shipped 1000 lamps, they could be packaged in 1000 one-pack boxes or 500 two-pack boxes and I figured how much volume that would be for both options in cubic inches. Then, because it seemed easier to visualize in cubic feet than in cubic inches, or even in cubic yards, I converted. (Full discloser: I used an online converter.) Here are those stats.
1000 lamps in one-pack boxes: about 116 cubic feet or 4.3 cubic yards
1000 lamps in 500 two-pack boxes: about 147 cubic feet or 5.4 cubic yards
My Mind Turned to Wondering
Then I wondered how much of a space saving two smaller squat boxes are over one two-pack box. I’ve always hated percent problems like these.
I also wondered if that’s why they made the switch and reengineered the stem of the lamp.
Then I wondered about how much cardboard they’d need for each box and would there be a saving there, too. I figured their surface areas, not adding extra for the flaps that allowed the boxes to close securely. Not much of a savings here.
One-pack surface area: 208 square inches for one lamp or 416 square inches for two lamps
Two-pack surface area: 432.6 square inches
And then I wondered about the shape of containers on ships and what makes for maximal packing. But I didn’t go there.
My Mind Turned to Classroom Instruction
Finally, I wondered about how I might use this in the classroom. Volume is part of the fifth-grade math curriculum, after students have engaged in the earlier grades with linear and area measurement. Fifth graders and middle-school students are expected to understand volume measurement and solve real-world math problems involving volume. Could my experience be turned into a classroom math investigation? Would I use customary or metric units? I have to do some thinking about how I’d structure that in the classroom. Stay tuned.
One Last Thought
I’m nervous about my calculations. I checked them over but have that feeling of worry that I remember as a student that I did something stupid when I figured, even though I used a calculator and an online tool. That’s a good reminder of how students often feel. And a reminder to be generous when listening to students’ reasoning.
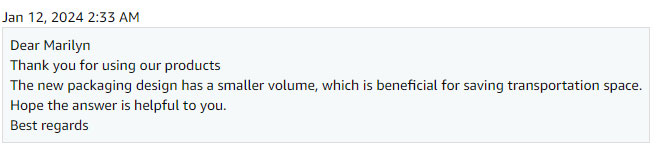
P.S. I Contacted the Lamp Manufacturer and just received this reply. So part of the math mystery is solved.