I’m always on the lookout for math experiences that engage students’ interest and curiosity, encourage them to persevere when solving problems, and are accessible to students with a wide range of abilities. Solving KenKen puzzles does all three. After getting hooked on solving them myself, I explored their classroom potential, and I’ve been pleased with the results.
At first glance, KenKen puzzles look like Suduko puzzles—you fill a grid with numbers. Both are logic puzzles, but KenKen puzzles have the instructional benefit of providing practice with basic facts. Plus Ken Ken puzzles are ideal for differentiating instruction. Now I’m hooked, not only on solving KenKen puzzles, but on using them with elementary and middle school students.
KenKen Puzzles Come in Different Sizes
In KenKen puzzles, the numbers you’re allowed to write to fill the grid depend on the size of the grid. If the puzzle is a 3-by-3 grid, you can use only the numbers 1, 2, and 3. If the puzzle is a 4-by-4 grid, you use the numbers 1, 2, 3, and 4. For a 5-by-5 puzzle, you use the numbers 1, 2, 3, 4, and, 5. And so on.
Getting Started in the Classroom
In the classroom, I post a puzzle for everyone to see. I choose an easy puzzle for a first experience. After I give some instruction about the Basic Rule and how to use the Number Clues (see below), I have students come up, fill in numbers, and explain their reasoning. Here’s a 4-by-4 KenKen puzzle that involves only addition. (The KenKen website directs you to puzzles of all levels.)
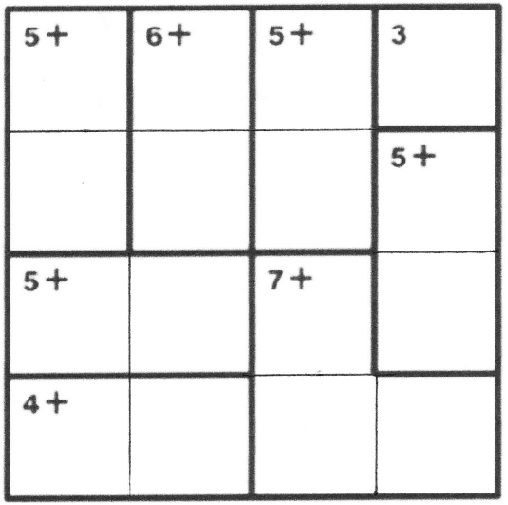
Basic Rule
I explain the Basic Rule: When you write numbers in a KenKen puzzle, make sure that you don’t repeat a number in any row going across or in any column going down. (The good news is that you don’t have to worry about the numbers on the diagonals, only about the numbers in the rows and columns.) You complete the 4-by-4 puzzle above by writing the numbers 1, 2, 3, and 4 in each row and column.
Number Clues
I also explain how to use the Number Clues to figure out where to write numbers, and this is where practice with basic facts comes in: Each area in the puzzle that’s outlined with dark lines is called a cage. There are eight cages in the puzzle above, each with a number written in the upper left corner. These are the Number Clues.
Outlined one-box cages are freebies, and the Number Clue is the number to write in that box. But when an outlined cage has more than one box, there’s also an operation sign after the number. The numbers you put in those boxes have to produce the answer that’s the Number Clue.
Since this is an addition puzzle, there’s a plus sign after all of the other numbers. For example, the cage in the upper left has two boxes and “5+” in it. That means you can fill those two boxes either with 1 and 4, or 2 and 3. Deciding which addends to use and in which boxes to write them is the challenge.
Try solving the puzzle.
From a Third Grade Class
As students seem ready, I introduce more difficult KenKen puzzles. Here’s a 5-by-5 puzzle that involves multiplication and division. I presented this puzzle to a third grade class. (The puzzle is a screen shot from one of the videos below, so it’s a bit fuzzy and the division symbols look sort of like plus signs. But there aren’t any plus signs in this puzzle, only times and division signs.)
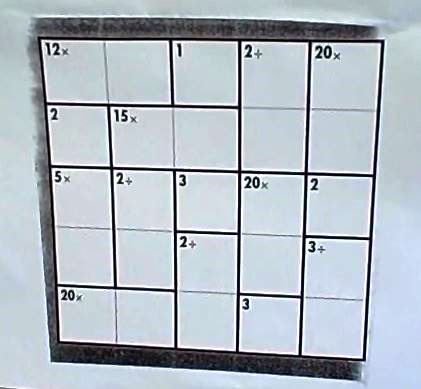
For this puzzle, watch the video clips of the first three students I called on enter numbers and explain.
We continued until the puzzle was complete. Then, as a class, we checked our results. I posted suggestions for students to refer to, encouraging students to do a three-part check when they think they’ve solved a KenKen puzzle.

Note: For a 3-by-3 KenKen puzzle, the numbers in each row and column add up to 6; for a 4-by-4 puzzle, they add up to 10; for a 5-by-5 puzzle, they add up to 15; for a 6-by-6 puzzle, they add up to 21.
A Final Note
I’ve found that some students like to work on KenKen puzzles on their own, while others prefer to collaborate with a partner. I let them choose which they’d rather do. Also, puzzles are ideal for sending home so students can teach their families how to solve them.



I LOVE your suggestion of having the students come up and fill in the numbers while telling their reasoning! I’ve only done this individually, or working together at their tables, never thought of it as a whole group activity! Thanks for this great addition. Teachers, you can sign up at the http://www.kenkenpuzzle.com/teachers/classroom site and have a variety of KenKen’s emailed to you weekly!
I’m so glad you’re keen on these too, Marilyn. I get my weekly set of them emailed from the KenKen people, so I’ve got loads now – great resource!
I also get these emailed weekly. My year 9 class, all 31 of them, are addicted to them.
I love these! Have you tried Kakuro? They are similar to KenKen except that the puzzles look more like a crossword puzzles in shape. My students (yr 5-6) preferred them to Sudoku because they involved some calculation. What I love about these types of puzzle is that as students become more familiar with them they begin to instantly recognise the possible sets of numbers. It was a given in my class that students verbalise their strategies and justify their solutions – I never confirm right or wrong.
Thanks for the tip about Kakuro.
Thanks so much for sharing the videos. I have heard about KenKen puzzles but had not seen them used in a classroom. I am an instructional coach and I can’t wait to share them with the teachers I work with.
I wonder if students could make their own KenKen boards. Well, really I wonder: If they were given such a task, then how would they proceed?
One way is just to fill out a 4×4 grid so that the frequency constraint is satisfied; partition it as you see fit; choose an operation for each region; compute the number for each region; and, finally, erase the numbers that were initially placed. Without concerning oneself too much with uniqueness, this is an effective way to make the boards.
But I imagine this is not how (many) children would begin the board designing process…
Some students happily make up problems, mostly as you describe. But in general, most seem to prefer to solve than create. I’d be curious to hear from other teachers about this.
I also am a big fan of KenKen puzzles. KenKen also has an app that provides puzzles to students. Initial puzzles are free. NCTM also has a game Math2 that has similar problems. This game is an app as well. More information on Math2 can be found at http://isolveit.cast.org/home.
Thank you!
My students love KEN KEN.
I have tried KenKen with my grade 2 students. They struggled with NOT repeating the numbers in each row and column. I stopped because I thought they weren’t ready developmentally, and it was only the easiest, 3×3 addition problems. Now, I’m thinking I was wrong and I should teach them differently. Really, they understood everything except to not repeat the numbers. What am I supposed to think about this?
I find that there is always confusion when I introduce something new to students. When I revisit something, after a little time, things seems to settle in. Keep me posted.
I have tried this my high school students that are well below grade level. One obstacle of success is that I can’t get them to keep themselves from guessing which number goes where in a cage. If a cage contains 2 numbers that add up to 3 they will put 1 and 2 in the boxes with no regard to checking if they can verify those positions are correct. I have tried so hard to get them to only place numbers until they know it is correct. I’ve showed them how to put 1 and 2 as placeholders until they can know for sure. My sense is they can’t go down a path and not write an ‘answer’. The idea of knowing it is 1 and 2, but not ‘answering’ and moving to another part of the puzzle to try again goes against what they think is the right way to solve a problem. The rub is when I work with them and make them back up and not fill it in until they know for sure they get annoyed with me when it turned out to be correct. Why did I make them do that, when they knew the right ‘answer’? Other times, when it doesn’t work out they can’t connect the dots back to a number placed without knowing for sure and causing problems later. This is also true for sudoku. The more I dig, the more I feel it has to do with getting ‘answers’. They see each choice as an isolated event and must make a decision and be done. I am trying to use more open problems that have more than one correct answer or tasks that you have to get wrong before you can get it right so they can get that feeling of backing up and trying something different. They still can’t seem to use what didn’t work to inform trying something new that would be in keeping with the isolated event thought process. Is this unusual? I used 4 by 4 easy puzzles with addition only. Am I not giving it enough time? Each year I’ve tried it, I ultimately gave up because they did not enjoy working on them at all. I do not even try sudoku because they are usually already familiar with them and hate them.
It seems that getting right answers is what’s comfortable for the students, so the puzzles are more frustrating and/or annoying than interesting. If the students aren’t interested in engaging with them, I don’t think it makes sense to push them. Maybe their already negative feelings about Sudoku are carrying over here. The only advice I can think of is to try introducing them with a light and playful approach, and if it doesn’t take, move on. You may find a class that’s more receptive, so don’t give up completely. Just don’t push if it’s more struggle than success.