To begin Good Questions for Math Teaching, K–6, Peter Sullivan and Pat Lilburn list three features of the good questions they’ve included in the book. These features sing to me.
- Good questions require more than remembering a fact or reproducing a skill.
- It’s possible for students to learn by answering the question.
- There may be several acceptable answers.
Then they provide more than 300 questions organized into 16 topics (money, fractions, decimals, place value, counting and ordering, operations, weight, volume, area, time, length and perimeter, locations and position, two-dimensional shapes, three-dimensional shapes, chance, and data) with questions for each topic organized into Grades K–2, 3–4, and 5–6 (except for decimals where there are questions only for grades 3–4 and 5–6).
I looked at the questions they posed for operations, the cornerstone of the K–6 math curriculum. Here’s a sampling of the 23 questions they included for that topic, with rationales and tips for using each.
Grades K–2
1. A basketball player scored 9 points in two games. What could her scores in each of the games be?
This question helps children think about a problem for which there’s a range of possible answers. For young children, decomposing numbers within 10 is an important reasoning strategy. There are ten possible answers, for whether the players scored 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9 points in Game 1. Changing the number of points is a way to tailor the question for individual needs.
2. I put some counters into groups with the same number in each group. I can’t remember what I did, but I do remember that I had 12 counters. What might the groups have been?
It’s important to supply children with counters to work on this question. There are four possible answers―two groups of 6, three groups of 4, four groups of 3, and six groups of 2. It’s fine if children don’t report all four possibilities, but for an extra challenge, you might ask a child to find all of the possible answers.
Grades 3–4
1. Five numbers added together make an odd number. What do you know about the numbers?
This question highlights some features of odd and even numbers. I love a question like this that both provides the opportunity to do a good deal of calculating, with numbers chosen by the child, and also asks children to make a generalization. In order for the sum to be odd, either one, three or five of the numbers must be odd. Would that also be true if the question were to explore six numbers that add to an odd sum?
2. What might the missing numbers be?
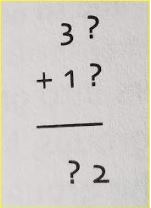
Again, this is a question that shows children that problems often have more than one answer. There are a variety of possibilities for choosing the missing numbers in the ones place for the addends, as long as they then determine a sum that has a 2 in the ones place. For a challenge, ask children to find all possibilities, or perhaps three or five possible solutions. If this problem is appealing, you might try a game version I described in a previous blog post: Four Strikes and You’re Out. I’ve found that’s always a favorite.
Grades 5–6
1. A school has 400 students. They all come to school by bus, and each bus carries the same number of students. How many students might there be on each bus?
This question doesn’t tell how many buses there are. That’s an open issue. When I watch children work on this, I’m interested in whether they use multiplication or division. My goal is for them to be able to use both and understand the inverse relationship between multiplication and division. For an easier version of this question: The answer to a division question is 5. What might the question be?
2. (a) How could you calculate 23 x 4 on your calculator if the 4 button is broken? (b) How could you calculate 23 x 21 if the 2 button on your calculator is broken?
The (a) question helps reinforce the relationship between multiplication and addition and most students press 23 + 23 + 23 + 23 = to get the answer of 92. But that’s not the only way. I’ve found that children who give that solution don’t typically think there are other ways, for example pressing 23 x 2 + 23 x 2 =. After showing this alternative, they may be able to find other solutions. The (b) question is typically more challenging.
At the beginning of their book, the authors give tips for making up what they describe as good questions and also describe how to use good questions in the classroom. These will be useful when you’re back in school with your students.
And for middle school students, there’s a companion book written by Lainie Schuster and Nancy Canavan Anderson.


