Confusion typically occurs in the classroom when I teach a new game to students. I’ve learned to be patient as I help students become comfortable with what they’re expected to do, but I’m always looking for ways to reduce the confusion hump.
When I recently introduced fourth graders to the multiplication game of Pathways, I tried a new approach. I organized the rules into four phases, easing the class into how to play by starting with a simple version of the game and adding information in manageable chunks.
It worked! Here’s what I did.
Phase 1: Teach what a pathway is.
On the board, I drew a grid of four rows with five squares in each.
I told the class that I was going to teach a game that was sort of like Tic-Tac-Toe. (In this way, I was connecting new learning to something the students already knew.) I explained that this game was called Pathways.
I pointed to the grid on the board and explained, “To play, you take turns marking squares, trying to make a pathway on the grid, either from the top to the bottom or from one side to the other side. Whoever completes his or her pathway first is the winner.”
I gave additional information, “Two squares are considered to touch if they have a common side or a common corner.” I drew three more grids and illustrated some possible winning pathways.
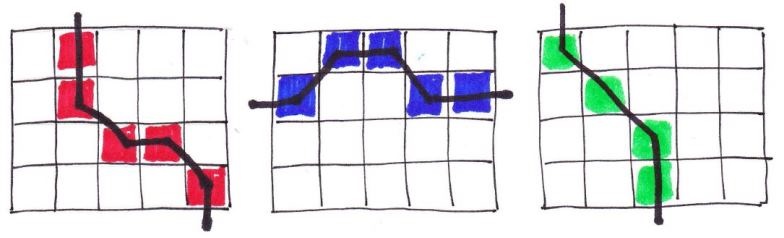
Then I modeled playing the game with Sara Liebert, the class’s regular teacher. Instead of using X’s and O’s as we do for Tic-Tac-Toe, we wrote our initials in squares, each with a different color marker. We played several games to help the students see how pathways can be created. The students loved watching Sara and me play against each other. They offered suggestions, groaned when one of us made a move they didn’t like, and cheered when one of us won. (It’s important to play enough times for students to get the hang of what it means to complete a winning pathway.)
Phase 2: Introduce products into the game.
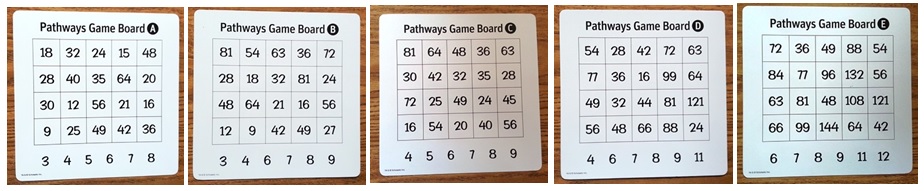
I reproduced the Pathways Game Board A, one of the five game boards available for playing the game. I enlarged it so everyone could see it and made two copies so I could demonstrate two games. I posted one copy on the board.
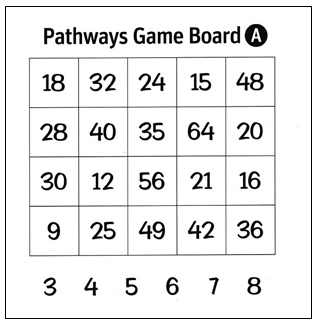
I introduced a new rule for playing on this game board, “You can mark a square on the grid as long as you can think of two factors that you can multiply to get the number in the square.” Students have multiplication tables available to them and were free to refer to them to help identify correct multiplication problems.
Hector asked, “What are those numbers at the bottom for?”
I responded, “We’ll ignore them for now until you feel sure you understand how to play the way I’ve described.”
Again, Sara and I played, engaging the students by having them suggest moves. They had lots of opinions. At times, we stopped and had them discuss what made sense to do next, and then we’d continue play. Also, we modeled recording a multiplication equation for each of our moves, preparing them for how they were going to play.
Phase 3: Introduce using factors for the game.
I asked them if they thought they were ready to learn another rule they had to follow in order to play Pathways. They were eager. “It’s about those numbers that Hector asked about,” I said, pointing to the row of numbers below the grid—3, 4, 5, 6, 7, and 8. “For this game board, those are the only factors you are allowed to use.” We looked at the multiplication equations we had written and agreed that Sara and I had made all legal moves.
Then I pointed to the number 40 in the second row of the grid. I asked, “What multiplication equations would allow me to mark the square with 40?” Hands shot up and I recorded their two suggestions—8 x 5 = 40 and 10 x 4 = 10. I then pointed out, “I couldn’t use 10 x 4 because 10 isn’t listed as a factor below the grid.” To be sure students understood so far, Sara and I played another game on the second copy I had made of the game board. The students’ involvement remained high.
Phase 4: Introduce the final rule about selecting factors
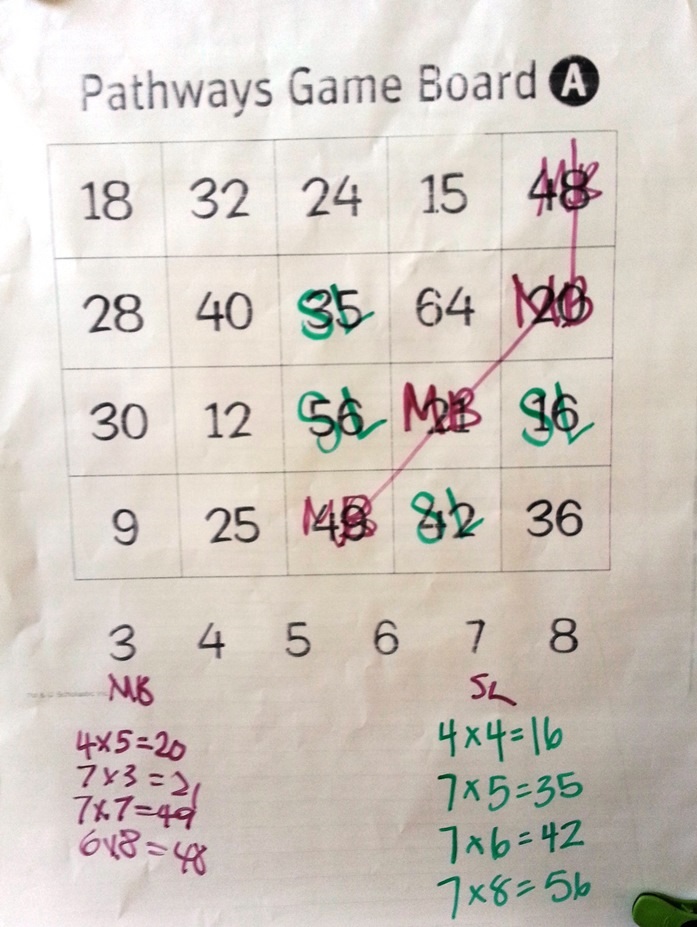
“There’s one more last part to the rules,” I said. “The first player chooses two numbers from the row of factors underneath the grid, marks the square with the correct product, and records the multiplication equation. Then, the next player has to use one of the factors the first player chose, change the other factor to a different one, mark the square with the new product, and record the multiplication equation. Each time you play, you have to use one of the factors from the previous play and change the other.”
I referred to the game we had first played to show them an illegal move. I pointed as I explained, “I began by playing with 4 x 5 = 20. Then Ms. Liebert changed the 5 to another 4 and played 4 x 4 = 16. Next I played 7 x 3 = 21.” I explained why my last move of 7 x 3 wasn’t allowed. “Choosing 7 x 3 isn’t a legal move because I changed both factors. In the real game, I have to leave one 4 and change one to another factor that’s on the list.”
It was the end of the time for math, so we told the students we’d start the next day with them playing the real game in pairs.
Day 2
The next day, Sara explained to the students that they would play in pairs. She showed them the materials they would be using,  which included Pathways game boards, green and yellow tiles to place on products, and two paper clips that they would use to mark the factors as they chose them. She showed them the five different versions of the game boards, pointing out that the factors and products were different on each of them. And she had two students play as the others watched to help everyone understand what they were to do. When the students were seated with their partners, Sara circulated, giving support as needed.
which included Pathways game boards, green and yellow tiles to place on products, and two paper clips that they would use to mark the factors as they chose them. She showed them the five different versions of the game boards, pointing out that the factors and products were different on each of them. And she had two students play as the others watched to help everyone understand what they were to do. When the students were seated with their partners, Sara circulated, giving support as needed.
As she circulated, Sara reminded students that each time a student places a tile, both should record the multiplication equation. This helps reinforce the multiplication facts.
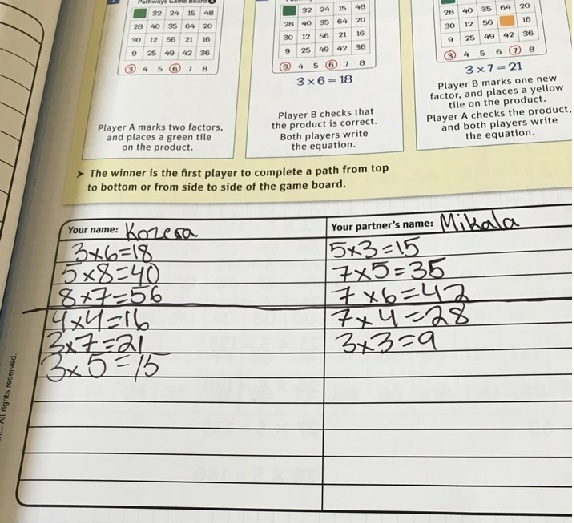
The students were completely involved playing. Because there was an odd number of students in class, Sara put three together and had two play against one. It worked fine. Here the two paired together gave each other a high five for winning a game.

Pathways Game Boards
Pathways is included in the Do The Math intervention program in Multiplication, Module B, with sturdy game board cards, tiles, and recording sheets. The game with reproducible game boards is also included in Teaching Arithmetic: Lessons for Extending Multiplication, Grades 4–5, a Math Solutions resource that I wrote with Maryann Wickett.


Great game! I love the factor selection game mechanic. We used small rubber bands to show which factors had been selected, on each turn, the player moves one band to a new factor.
At each stage in the explanation, the games you described were worthy games in and of themselves. As a follow-up, I would encourage the kids to play each version and share their thoughts.
I wonder about the arrangement of the labels in the squares. Is there a pattern and/or underlying reason or was it random? We have thought a little about the resulting differences in game play from the factor game based on different arrangements of labels, but didn’t arrive at any conclusions.
It makes me think of Optimal Dartboard, which I only saw recently because of 101 Questions.
I honestly can’t remember the reasoning behind how we placed the products in the squares, so I can’t help there. Thanks for the links to Optimal Dartboard and 101 Questions.
Is there a mathematical reason that the board is not square; that is is 5 x 4 rather than 5 x 5?
No reason. I think a 5 x 5 would be fine. Give it a try and let me know.
I am curious if you, or anyone, has created a pathways board for division facts.
Hmmm, I’m not sure about Division Pathways. If you figure out a game, please let me know. I like playing Division Bingo — maybe I’ll do a blog about it.
Has anyone ever Pathways with a board with a some negative numbers? I wonder how the game could play if, for example, the gameboard had half of the numbers as negatives?? Any thoughts?
Hmmm. I hadn’t thought about this. Please let me know if you try it. I’m always looking for ways to expand and extend games.
Can someone please help and clarify for me?
I noticed that the rules on the printed version that I printed from mathsolutions.com state that the pathway has to be from left to right however the blog says that it can be from top to bottom or left to right.
When we play left to right only, the students actually get “stuck” and there are no possible moves.
Initially I suggested that this player would miss a turn and hopefully on the next turn they might be able to move. The problem however is that there are times that both players get “stuck” with no possible moves.
I’m also playing it so that the path must be continuous and not disjointed and that they can’t go back to their initial starting square and start again, meaning that the path goes back on itself.
Are we playing it incorrectly?
Thanks, Rachel, for your comment. There’s never just one way to play any game. The rules that I like using appear in Teaching Arithmetic: Lessons for Extending Multiplication, a book that I wrote with Maryann Wickett, and in Do The Math. I don’t require that students play from left to right. Also I don’t require that the make the path continuous, but allow them to make what I think you’re referring to as disjointed paths. That seems to add more excitement to their strategies. But whatever the rules, most important is that the students understand them. And enjoy playing. Let me know if I can provide any other information.