This school year, I’ve been working with a class of fifth graders, partnering for math with their teacher, Aimee Levin. I recently engaged the students in a card sort where they worked in pairs to match division word problems and possible answers. The numerical problem was the same for all of the word problems: 21 ÷ 4. I chose these numbers because I knew they would be numerically accessible and allow the students to focus on the contextual situations without also having to grapple with the math.
To prepare the class for the card sort, I engaged the students with the idea that a division word problem might have more than one possible correct answer. Here’s what I did.
Setting Up the Card Sort
I began the lesson by telling the class this story, “Three students found a small cloth bag that had four quarters in it. They took it to their teacher. No one in the class claimed it, so their teacher asked them to take it to the principal. He asked all of the teachers in the school to check with their students, and still no one claimed it. The principal told the three students who found the bag that they could keep it and that they had to share the contents equally.”
Then I posed a question and wrote it on the board:
If 3 students equally share 4 quarters, what does each student get?
Before asking for answers, I asked them to mathematize the problem, that is, to tell me what math problem I should write on the board for this story. One student suggested 100 ÷ 3 and explained, “Four quarters is one dollar, and that’s 100 cents, so they have to share 100 cents.” Another suggested 4 ÷ 3 and explained, “They have to divide up the four quarters for the three of them.” A third suggested 4 quarters ÷ 3 and explained, “It’s kind of like the other one but my problem tells what they’re sharing.”
I recorded their suggestions on the board:
100 ÷ 3
4 ÷ 3
4 quarters ÷ 3
Next, I asked them for answers and they suggested four:
33¢
4/3
1 r 1
25¢ r 25¢
Then I rephrased the question. I crossed out “what” and wrote “how much money” above it. I read the revised problem aloud, “If three students equally share four quarters, how much money does each student get?” I then asked, “For this question, which of the four answers on the board are correct solutions?”
The discussion was interesting. They agreed that two of the answers could work―either 25¢ r 25¢ and 33¢. One girl explained, “They could each get 25 cents and there would be 25 cents leftover.” Another added, “If they cashed in the last quarter, they could each get 33 cents and there would be a remainder of 1 cent.” There was disagreement about the other two answers on the board, with some thinking that they could be OK answers but that they didn’t match the question about “how much money.”

This is the board work for the problem of 3 students equally sharing 4 quarters.
Introducing the Card Sort
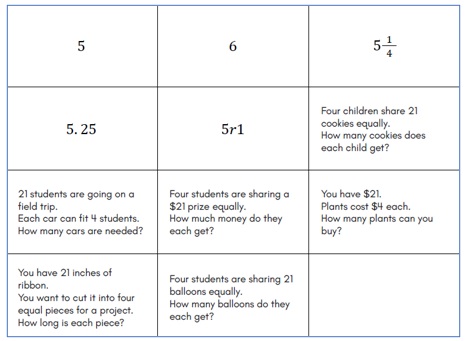
I then held up a sheet of the cards and asked, “If I cut these apart, how many cards would there be?” They easily determined that there would be 12 cards. Here’s the Card Sort PDF.
“Not really,” one girl said, “there’s a blank.”
“Yes,” I confirmed, “and you’ll learn about what to do with that in a moment.”
Then I explained, “You and your partner will get one of these sheets already cut apart so that you’ll have 12 cards. There are five answer cards (I pointed out the cards with numbers), six problem cards (I pointed out the cards with word problems), and one blank card. Your task is to match the problems with the answers. There’s one more word problem than there are answers, so an answer can be used more than once.”
A pedagogical note: Rather than tell them that a problem card might match more than one of the answer cards, Aimee and I decided that we’d not reveal that idea and see if it emerged as they work. Then we’d confirm that a problem card could be matched with more than one answer card.
One girl asked, “What do we do with the blank card?”
Another piped up, “We could write our own problem.” That was exactly the task I had in mind for pairs that finished more quickly. I confirmed, “If you have time, write a problem on the last blank card that can match one of the answer cards.”
The students engaged immediately with the task and pairs worked in different ways to sort the cards. Some pairs divided cards so one took the word problem cards and the other took the answer cards and worked through each problem together. Other pairs spread out all of the cards and looked for matches. There was a good deal of interaction and the room was noisy, but the noisy conversations felt productive. About half of the students had time to write their own problems before I interrupted them and switched to a follow-up activity.
Revisiting the Plant Problem
When I had their attention, I told them, “Look at your cards and find the problem about buying plants.” When they had found it, I asked one of the students to read it aloud: You have $21. Plants cost $4 each. How many plants can you buy? Before class, I had written this problem on the small portable whiteboard.
“Let’s revisit this problem,” I said. I brought their attention to the small whiteboard and below the problem I had written, as they watched, I set up a table with five columns and labeled them: # of plants, Cost, $ leftover, Remainder, Answer.
“Suppose you bought just one plant,” I said. “How much would that cost?” They answered in unison, “Four dollars.” I recorded 1 in the first column labeled # of plants, and in the next column labeled Cost, I wrote: 1 x 4 = 4.
A pedagogical note: I had first considered writing only the cost but then decided that this was an excellent opportunity to model using multiplication as we thought about a division problem.
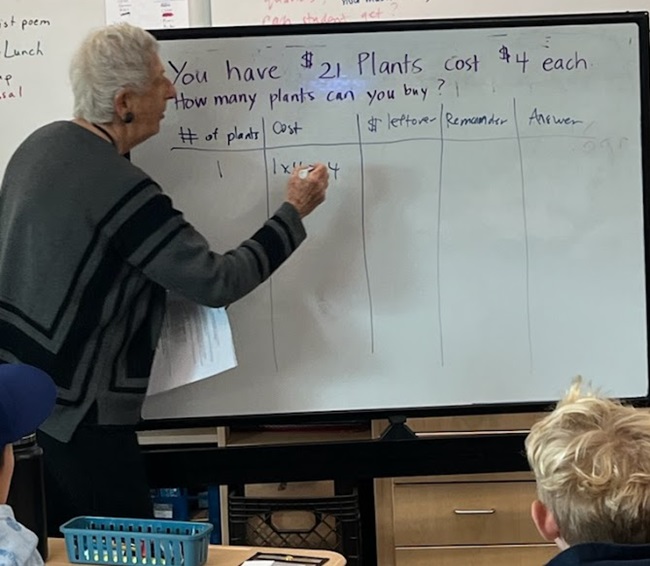
I introduced the idea of using a table to analyze the plant problem.
With the students’ input, I continued to record on the table. The math they struggled with most was doing the subtraction to figure out the remainders. Two problems, 21 – 8 and 21 – 12, were challenging for them. Also, when I wrote 6 in the first column, there was a burst of conversation. “You don’t have enough money.” “You could see if they would sell it for $1.00.” “Maybe you could borrow more money.” “You’d have to borrow $3.00.”
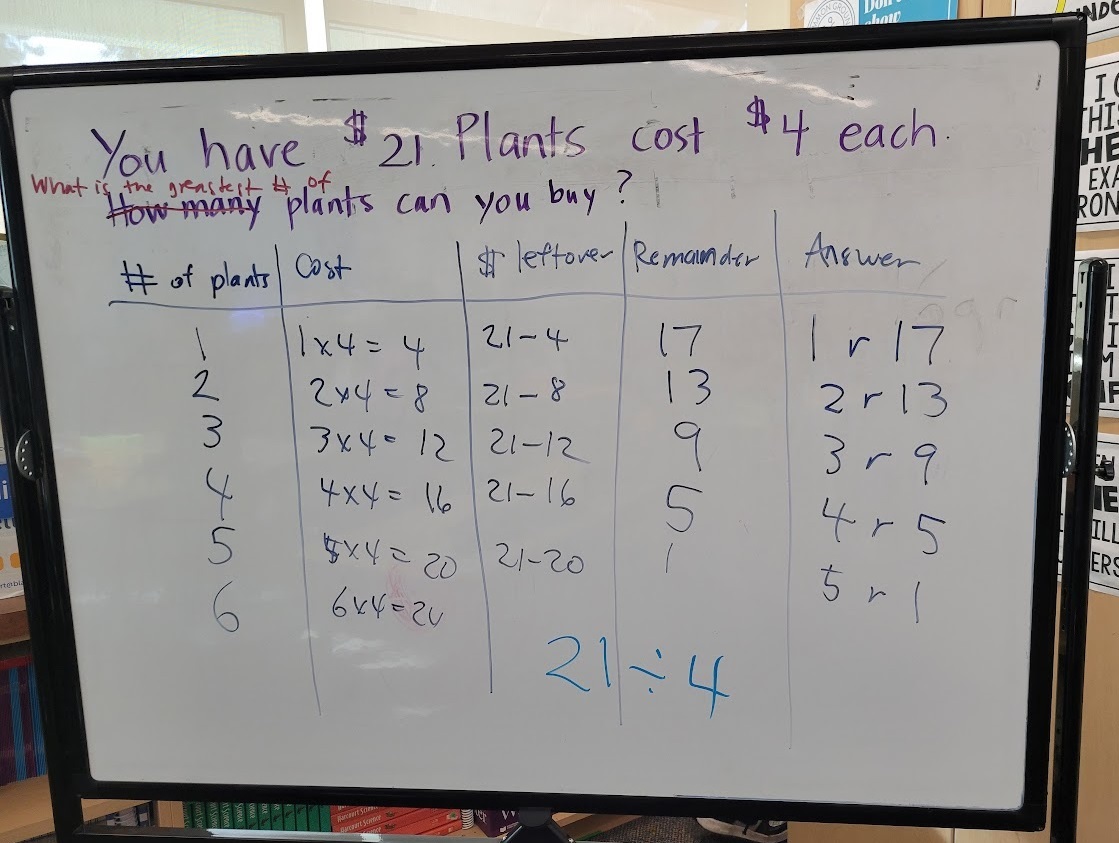
This is the table completed with all of the information.
I wrote the numerical problem we were solving below the table: 21 ÷ 4. I said, “So we have five different possible answers for the plant problem.” I pointed as I read each of what I had recorded in the Answer column.
Then I said, “Watch as I revise the question.” I crossed out How Many, wrote a replacement, and read the revised problem: What is the greatest # of plants you can buy?

I then asked, “Which of the answers work for this question?” I had them turn and talk with their partners and then led a discussion. They agreed that 5 was the greatest number of plants they could buy with $21.
One student said, “It could be 5 or 5 remainder 1.”
I thought for a moment and then asked, “I know that the 5 means that you can buy 5 plants, but what does the “remainder 1” mean if you include it in the answer?” A buzz broke out and they agreed that the answer could be “5 plants” or “5 plants with a remainder of $1.00.”
A pedagogical note: It’s valuable to revisit answers to word problems to hear students explain what the numbers mean. It’s often hard for students to describe the meaning of remainders.
For what I did with the class to follow up this experience, read my next blog.
__________________________________________________________________________________________________
How I Learned About Card Sorts
About a dozen years ago, I was fortunate to attend a workshop led by Malcolm Swan, who was working at the time with the Shell Centre in Nottingham, England. He engaged us in a card sort that focused on linear functions. The task was to connect equations and graphs. I was inspired by the idea but never took the step of using card sorts with the classes I was teaching. (I think this has happened with many good ideas I’ve learned about.)
Thanks to Others for Helping Me Plan
I often reach out to colleagues to help me think through instructional decisions. I planned this lesson with Jenna Laib and when she suggested doing a Card Sort, I immediately agreed. Together, Jenna and I designed the content of the cards, and Jenna made the Card Sort PDF that you can access if you’re interested in trying this with students. Thanks also to Henri Picciotto for suggesting that I include “6 plants” as an option on the table. I didn’t take it very far, but it might be interesting to think about negative numbers. And thanks to Karen Economopolus for reminding me of the importance of asking students to interpret remainders rather than assume they understand their meaning.

How much fun to be in a math class with you. Lucky kids!
I enjoyed reading this lesson outline very much. I love the ‘pedagogical notes’ explaining the reasoning behind the decisions made.