This morning, I read a comment posted in response to my recent blog, Eleven Things about the Number Eleven. MQ referred to the very last entry in the extra page of math facts about 11 that I printed separately and rolled into a scroll to accompany the book I made for my grandson’s birthday.

I had found this math fact about 11 on the internet when I was creating the book. While it caught my interest enough to include it, I didn’t think more about it. But now I was curious.
I tinkered some with other pairs of numbers, as MQ did. For every pair of numbers I tried, where one number is 1 more than the other, the sum of the numbers was equal to the difference of the squares of the numbers.
To think about this, I made a sketch.

The green square is 5-by-5, which is 52. (I still remember how amazing it was to realize that 52 related not only to 5 x 5, but also to a 5-by-5 square.) The blue-ish square, most of which is hidden behind the green square, is 6-by-6, or 62. So the difference between them is the part of the blue square that’s showing, its top row and left column, which has 11 units. And that’s 6 + 5 units. Or 5 + 6 units. Or 5 units + 5 units, plus the extra corner unit. Which is the 11 from the book I made from my grandson.
So, I concluded that for any two squares, where the length of the side of one is 1 more than the length of the side of the other, the difference in their areas would be sum of the lengths of the two sides.
I also thought about it using algebra. Here’s what I wrote, using n and n+1 to represent any two consecutive numbers (5 and 6 in the example above) and 2n + 1 to represent their sum (11 in the example above).
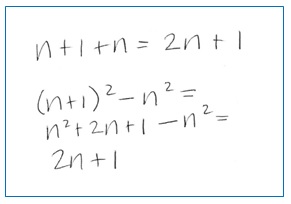
In the spirit that writing is how we work ourselves into a subject and make it our own, writing this blog has helped me make sense of why the math fact I included in my grandson’s book holds true for all pairs of consecutive numbers.
But I realize that this blog might be useless to others reading it. What I’ve done is given an explanation that falls into the category of “teaching by telling,” which I avoid in the classroom when I want students to “uncover” knowledge that’s based in understanding relationships. This is in contrast to when I feel I need to “cover” material that’s based in social convention, not logic. (For more about this, read the comment I posted on Dan Meyer’s provocative blog, An Advocate of Explicit Instruction Experiences the Limits of Explicit Instruction.)
I know I’m rattling on a bit. But I needed to share my excitement at making a new math discovery.
So . . . what about if we thought of 11 as 7 + 4, numbers that are 3 apart. Then what about 72 – 42? Well, it’s not 11. It’s 49 – 16, which is 33, which is 3 times 11. Hmmm, there’s more to tinker with and discover.

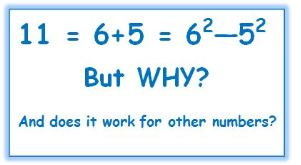
Is it fair to give a hint? Think a^2 – b^2
Also, your note got me to think about a geometric representation of the factorization, similar to your greenish/bluish squares. It is nice and I’m surprised that I hadn’t ever thought about it before.
I think that utterly throwing out “teaching by telling” is a silly idea, especially since I already have learned the thinking practices that let me learn by listening 🙂
I agree that “utterly throwing out teaching by telling” doesn’t make sense. But when knowledge is grounded in logic, not merely convention, it’s important to provide students ways to interact with that knowledge in a variety of ways — listening, actively investigating, talking to others, experiences with concrete materials, and more. I wrote about these ideas in an Ed Leadership article, Uncovering the Math Curriculum. Take a look.
A related idea: The sum of the first n odd numbers (1 + 3 + 5 + … + (2n – 1)) equals n^2. This is easy to see geometrically (1 = 1^2 can be represented by 1 square; 1 + 3 = 2^2 can be represented by a 2 x 2 square, with, for example, 1 red square and 3 yellow squares; 1 + 3 + 5 just adds 5 blue squares to make a 3 x 3 square, etc.)
What fun several minutes playing with your problem. Here’s what I thought
a^2 -b^2 = ( a+b)( a-b) and all of the numbers that you picked a-b =1 so the results had to work. Now seeing your further ruminations about numbers that are further apart will give me some more fun thinking.
I agree with you that kids should have a chance to play with this and see what they can come up with as well and how much fun it would be to listen to a class discussion where a bunch of ideas that are different (like your geometric solution) would be presented and considered.
I didn’t think anything about the original statement either until you posted this. Thanks for a reminder that there is much to be considered in most of the math we do.
In further investigating if the two numbers have a sum of 11, then the difference between them is a factor and that factor is an odd number. For example 9+ 2 = 11 the difference of the two numbers is 7 and that is a factor of the difference of the squares or 7*11.
When looking at other possibilities of numbers whose sum is 11, the difference of their squares is that difference between the numbers times the quantitiy 2 times the smaller number plus the difference of the two or a(2x+a), where x is the smaller number and a is the difference between the two numbers. I am sure that there are probably more patterns to be found.
The patterns seem endless! Thanks for these.
Lovely!
I’ve played with this too:
http://seekecho.blogspot.fr/2014/04/discovered-with-pebbles.html
It’s neat that when your L shape (the Greeks called it a gnomon, the bit that cast the shadow in a sundial) is a square number, you get the sides of a right angle triangle.
A practical application in arithmetic for some of the math represented above is to build a square knowing the square above or the square below the one you are looking for. If you know five squared is 25 and you want to determine six squared, you add 5+6 to 25 to get 36. This is an easier way for kids who have not yet had algebra to see the n^2 + 2n + 1 binomial expansion of (n+1)^2 or in the terms of the prior example (5+1)^2=5^2 + 2•5+1=25+10+1=36.
This also works with subtraction. If you know 10 squared is 100 and want to determine nine squared, you can subtract 10 and then nine from 100 to get 81.
Most of us know 20 squared, but not 19 squared from memory. 400-20-19 = 361 which is 19 squared. This is (n-1)^2 where n is equal to 20 and 20 squared – 2n +1 =
400 – 40 +1 = 361.
This reminds me of a 4th grade student a few years ago. When I asked him how he knew 7 x 9 equals 63, he explained that he used 8 squared is 64 and then subtract 1.
Thinking about this later on a long drive and trying it out with different numbers (4×6=24=5 squared – 1, etc.) I was able to best understand it for myself by using geometric arrays. Imagine a 5 x 5 array, then cut off a 1x 5 column to create a 5 x 4 array. Then rotate that 1 x 5 column to join the bottom of the 5 x 4, now creating a 6 x 4 array but with 1 extra cell dangling off the side. Cut that 1 cell off (subtract 1) to create the perfect 6 x 4 array.
Ah, another fine pattern.
You can find this same pattern discussed in my follow-up comment from the previous entry.
The comment:
https://marilynburnsmath.com/eleven-things-about-the-number-eleven/#comment-4209
Re-pasting one line here verbatim:
Here is an image transforming 3*5 + 1 into 4*4: http://i.imgur.com/k9n68im.jpg
Algebraically the example above of 7×9 = 8 squared minus one is a subset of a larger pattern. Whenever multiplying two numbers whose average is an easy number to square, you can use the expansion of (a+b) (a-b) to find the product. Another way to say that is “The two numbers are the same distance in opposite directions from a number that is easy to square.” For example, if we were multiplying 17×23, the average of which is 20 whose square is 400, we would use 20 as the “a” in the formula and use 3 as the “b” in the formula. (20+3)(20–3). The expansion of the binomial after simplification is a-squared minus b-squared, so this example would be 20 squared minus 3-squared or 400-9 or 391.
Thanks very much for this explanation.
Great post, with nice information