Below are examples from two fifth graders I interviewed. I asked each to use paper and pencil to figure out the answer to 5000 – 328. Both students got the correct answer of 4672, and it took both of them about the same amount of time to complete the work.
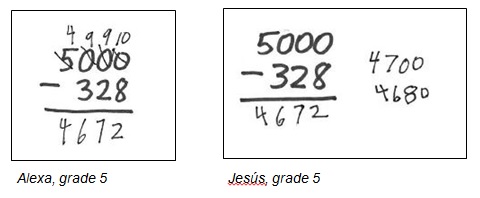
Alexa’s solution shows how she applied the standard algorithm that she had been taught. As she worked, Alexa gave clear explanations about the steps she used, demonstrating her proficiency with the procedure.
Jesús solved the problem in a different way. He didn’t explain as he worked. I watched as he thought for a moment and then wrote 4700 to the right of the problem. He thought some more and wrote 4680 underneath 4700. Finally he wrote the answer of 4672. When I asked Jesús to explain, he said, “First I did 5000 minus 300, and that’s 4700. Then I took away 20 more, and that left 4680. And then I subtracted 8 and got the answer.” Jesús didn’t use the standard algorithm but instead used paper and pencil to keep track of his thinking as he computed.
The standard algorithms that we teach are effective and efficient, and it’s important for students to learn and practice these paper-and-pencil procedures. But these algorithms aren’t the only ways to compute. Jesús’s strategy for subtracting, for example, also efficiently produced the correct answer. He was comfortable with his method and confident about the answer. However, I had never seen this strategy before and was more curious than comfortable or confident.
When I got home that day, I fiddled with Jesús’s strategy on a slew of other subtraction problems with whole numbers and found it surprisingly effective and efficient. (I suggest you try it for yourself.) Then I wondered if his method would work for subtracting decimals. Success! (Try it yourself and/or see if you can follow how I applied Jesus’s method to the problems below.)


Questions from Teachers
When I share Jesús’s work with teachers, they typically react as I did with surprise and curiosity—and some confusion. The following Q&A collection presents some of the questions teachers have raised as we investigated Jesús’s work and my responses. After these questions, I suggest some ways to use this experience in the classroom.
Q. Is Jesús’s strategy mathematically OK?
Yes. Jesús decomposed 328 into its place-value parts—300, 20, and 8. While his strategy of working from left to right isn’t conventional, it indicates that Jesús was able to apply his understanding of place value. (I’m not sure that I would have understood how Jesús had reasoned merely from looking at his paper and not listening to him explain. This is an example of why I find interviewing students so useful.)
Q. Is Jesus’s method an algorithm?
I think it is. An algorithm is a step-by-step procedure that provides a reliable and efficient way to compute for a broad class of problems. After trying Jesús’s strategy on other problems (see above), I’m convinced that I can use it for all subtraction problems, so I consider it a subtraction algorithm. A caution: When teaching algorithms, It’s important for students to learn how they are based on the structure and logic of our number system. It’s important for them to understand that algorithms are procedures that have been invented to carry out calculations we need to do repeatedly.
Q. Are you recommending that we teach students how to use Jesús’s strategy for subtraction?
No, I’m not recommending that students become proficient with Jesús’s strategy. However, as I describe in the Classroom Suggestions section at the end of this post, it would be valuable for students to think about why Jesús’s method works. This is a way to stretch their mathematical thinking, to strengthen their understanding of place value, and to give them another way to apply their place-value understanding.
Q. What’s the difference between a strategy and an algorithm? Why isn’t Jesús’s method a strategy, not an algorithm?
These are important questions. I googled “strategy vs algorithm in teaching math” and 12,900,000 results came up (in 0.63 seconds). In the context of arithmetic, when a strategy can be generalized to a systematic, step-by-step procedure for computing that works for a broad class of problems, then it can be considered an algorithm. Even though not all students’ strategies are algorithms, their strategies are valuable ways for us to assess their understanding and for them to develop, extend, or cement their learning.
Q. Can you give an example of a student’s strategy that isn’t an algorithm?
Take a look at this video clip of Amelia figuring out the answer to 100 – 18. I think it’s an example of a strategy that works for specific problems but isn’t as broadly useful as other algorithms for subtracting.
Q. We do expect students to learn the standard algorithm for subtraction, don’t we?
Yes. It’s also important for us as teachers to help students understand how algorithms are rooted in our place value system and are based in logic. For that reason, along with learning algorithms, I think it’s important to discuss why they work. Also, I think it’s important that students know that the procedures we identify as standard algorithms aren’t the only algorithms that exist.
Q. Could Jesús’s method be the standard algorithm recommended today instead of the one we current use?
I think that’s an interesting idea. As a child, I attended P.S. 225 in Brooklyn, NY, and learned how to subtract as a second grader in Miss Collins’s class. I remember learning what she described as the “borrow, pay back” method, which I guess was the standard subtraction algorithm taught then. It’s not the algorithm that’s currently considered to be standard, but another that’s also rooted in place value and based in logic. Later, in a teacher prep class on teaching elementary mathematics, I learned that it was called the Italian method or the equal addition method. I still subtract that way when I resort to paper and pencil (which is rare, indeed). (If you’re interested, do an Internet search for “equal addition subtraction method” to find lots of options for learning about what Miss Collins taught.)
Classroom Suggestions
Try these ideas for giving students ways to think about subtraction.
- Demonstrate Jesús’s method for subtracting. Ask students to make sense of why Jesús first wrote 4700, then 4680, and finally the answer of 4672. Give students the opportunity to explain Jesús’s reasoning in their own words. Then give students a subtraction problem and ask them to solve it using Jesús’s method. (Use either 600 – 582 or 4000 – 1635, problems that require students to subtract across zeros, which typically presents problems.) Have them work in pairs or small groups and then make up other problems to try. Lead a discussion about why the method works.
- When students use the standard algorithm for subtraction, they are renaming the top number in order to make the subtraction easier. While Alexa didn’t think about this renaming, she changed 5000 to 4000 + 900 + 90 + 10, which is equal to 5000. Understanding this calls for focusing on the why of the algorithm, not just the how. To help your students think about this, record on the board how Alexa solved the problem. Then ask students to talk in pairs or small groups about why the following is true:

- Here’s another way to represent the renaming that Alexa did to subtract. Show this to your class and have them discuss.

Final Note
For more about subtraction, read Yet Another Way to Subtract.

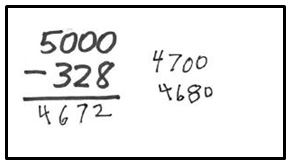
I wonder how he would have handled 5000 – 32?
I think it is likely Jesús was engaging more with the meaning of the numbers when doing his calculation and entirely possible Alexa was not engaging at all with that meaning. This is based on observing my own thought processes when calculating with the standard algorithms. Indeed, part of the point of algorithms is that they substitute procedure for understanding, hence their applicability in programming (and for novices in many skilled activities). For another example, euclid’s algorithm is a great method for calculating GCDs, but not helpful for understanding what a GCD is.
In application, I often use something like Jesús’s method as it has a key benefit: if you have to stop part-way through the calculation, your last calculation will be a close approximation to the answer (closer than if you had done the same number of operations in the standard algorithm). Also, there are plenty of times when it is much more important to know that 5000 – 328 is about 4700 than to know that the ones digit of the result is 2.
Similarly, it is easy to see 5000 * 328 is close to 1.5mm (approximating as 5000*300) or I would probably do 5000 * 330 = 1.65 million as get the extra precision almost for free (having already done a 5×3 operation and figured out the power of 10 of the largest digit).
Joshua
http://3jlearneng.blogspot.com
I tend to agree with Josh’s initial assessment. And I performed the calculation as 500 – 30 + 2.
I got your blog this morning and found it to be right on once again. Regarding the question of is it an algorithm–Yes! It is an ordered set of steps that resolves all problems of subtraction. The proof is in a series of messy place value decompositions combined with a number of reassociations of the parts and finally (basic facts) resolving of the indicated subtractions. However it is very efficient and related to several of the other left to right moving algorithms for addition and multiplication. Keep up the good work!
*Sometimes* the folks who whip through the standard algorithm are doing it without understanding, but not always 🙂 . I know I was expected to understand algorithms and being a verbal gerbil tried to figure out different ways to explain it. The ‘standard algorithm’ is more zoned in on one place value at a time than the alternative one but they both can be done with comprehension.
That said, too often once a student has the algorithm, they’re allowed to let the “smart people” answer the ‘why’ questions 🙁
I have found that some fourth graders love to use the constant difference method when subtracting from a number with zeros. For 5000-32, most of my students would say “I don’t want to work with all those zeros, so I will subtract 1 from both numbers, making the problem 4999-31. Then, the problem is simple subtraction, giving them 4968. Because I think this is so much faster and is easily computed mentally, I now apply this strategy. I would never ask a student to use the “U.S. Standard algorithm” on this problem if they use constant difference and understand why it works.
I think there is a place for algorithms, but I disagree that any one algorithm needs to be endorsed for students and “expected” to be learned by students. If they have an algorithm, or several strategies that are situational, and they are efficient and accurate, they have successfully developed number sense and there isn’t any need to push them into an algorithm that isn’t natural for them. I have had students who developed the standard algorithm on their own (or they had seen it before and adapted their understanding of place value to create the shortcuts themselves), so I do believe that standard algorithms are a natural progression in computations.
I agree with Jessica about finding a strategy that works for the student. The standard algorithm sometimes becomes a memorized process and when they get lost in the steps they don’t know how to solve the problem. I have had students that could show you how to do the standard algorithm and even tell you they were borrowing 10 but I soon realized they struggled with number sense and had been taught what to say as they went through the process. I have also had “math brain” kids that started using number strings. When they decomposed the numbers and then started the subtraction they soon discovered negative numbers (they used the number line on the wall) so we had to work on negative numbers. Then they started subtracting from the left (after all this is the direction we read and write). I usually had to interview them to make sense of their strategy so we designed a way to record it.
541
-253
300-10-2= 288 some of them had to add a step and would write 300-10-2= 290-2=288
One year 1 had a 4th grader that had struggled in math, especially subtraction. She just couldn’t “get” the standard algorithm. I told her to do what she thought would work for her. She brings me an addition problem. I had to interview her for most of the math class to understand what she was doing. she would set up her problem like this
253
+_______
541 She starts in the ones column and knows she can’t add anything to three to get a one so she has to add something to the three to get an 11. She puts an 8 in the ones column. She knows that the extra 10 needs to be added to the tens so she changes the 5 (50) to a 6 (60). Again, she knows she can’t add anything to the 6( 60) to get to the 4 (40) so she has to add a number that will add up to 14 (140). She puts an 8 in the tens place. And she knows she needs to add the 1 (100) to the 100’s column. She sees she can add a 2 (200) to the 3 hundreds that are there. She fills it in as she goes so it looks like an addition algorithm. I realize that it’s a missing addend but her understanding of how to manipulate the numbers made me realize she knew a lot more about math than she believed and she had a strong number sense. That wasn’t showing up when she was forced to use the standard algorithm. I was amazed (once she was able to explain her thinking). I was glad I had insisted the class find a different strategy other than the standard algorithm. I learned so much more about them as mathematicians.
I love teaching math and appreciate the work Marilyn Burns shares as she learns.
And Jessica, I also agree that the algorithm is a natural progression, it’s just another way to record the math. Neither of my own children knew how to do the standard algorithm until 6th grade (we were teaching Investigations at the time. My son came home from school one day and asked me to show him the algorithm because everyone else was doing it. I showed him and he said, “Oh that’s easy! It’s just another way to show your math.” Both of my children are very strong in math. I think a great deal of it has to do with our school focusing on understanding the “why” in math and having the students explain their thinking.
I am somewhat familiar with Jesus’ method. It is great and less confusing than the standard algorithm. However, it does require a certain level of math sense, knowledge of estimation, and understanding of numbers. When students do not have that prerequisite knowledge it requires more teaching. I think this may be the reason why so many teachers resort back to the traditional rote algorithm. Just my thoughts.
While this is more than a year old blog post, I just ran across it today and felt compelled to comment.
It is scary to me that math teachers don’t think mathematically. That the teacher had to ask the student what he was thinking. I am glad that this teacher took the time question the student, and was humble enough to learn from the student to think mathematically and then further to discuss it with other teachers and also write about it in this blog. Kudo’s for that humility and effort.
It took me all of 15 seconds actually looking at the Jesus graphic to figure out what the child was thinking. Perhaps that is because I too think mathematically, though I have never done a subtraction problem with such a method. I was also taught the “standard algorithm” as shown in the Alexa graphic. And hence I understand the reasoning why that works because I think mathematically.
However, just as commenter Joshua above notes, it is quite possible that if Alexa doesn’t think mathematically (has not been taught to think that way), she doesn’t understand the WHY the algorithm she was taught works, rather goes through the motions, of “borrowing” one from the next digit over.
The biggest problem I have with mathematics taught in school (hoping it will change some day), is that teachers who don’t think mathematically teach “algorithms” for arriving at the proper answer to “arithmetic” and the entire focus for Kindergarten to 7th Grade (sometimes even up through 9th Grade) is on arithmetic only without teaching any other branch of mathematics. Hence children don’t learn to “think mathematically” rather they are only taught to “perform calculations.”
What I like the most about the Common Core Mathematics Standards is that those who wrote the standards clearly think mathematically, and want to teach children to also think mathematically. Albeit the implementation of those standards is lacking for two clear reasons 1) those who write mathbook texts and problems [the big name publishers] don’t think mathematically, and 2) math teachers themselves don’t think mathematically. Which has caused so many parents to rebel at the idea of the Common Core Mathematics Standards.
So, someday, I hope the actual implementation of Common Core Mathematics will bring children and adults alike to think mathematically so that they can recognize at an instant things such as the obvious breaking down of place value in a subtraction problem.
I’ve just read all of your posts. Thanks so much for your thoughts and perspectives . . . and for taking the time to get them down in writing. Much appreciated.
Hi, My 7th grade pre-algebra teacher finally helped me conquer my struggles with subtraction. Have you seen this method before?
If the problem is 5000-39, I do the following:
Add 10 to the one’s place in 5000, and add one to the ten’s place in 39, then add 10 to the ten’s place in 5000 and add 1 to the hundred’s place in 39. So I would end up calculating the one’s place as “10-9” the ten’s place as “10-4”, and then finish with “50-1. “
If I understand your explanation correctly, it seems that each time you’re adding the same amount to both numbers (e.g. 10 in the first step) which keeps the distance between the two numbers the same. I like to think about the difference as the distance between the two numbers on the number line. Thanks for sharing.