Always Try a Problem Before You Assign It

Several caveats about this post. One is that it’s my first post in almost four months. (I took a long summer break.) Another is that it’s long, too long according to the conventional wisdom for making blog posts accessible. A third is that it’s sort of “mathy” in a way that’s different for me. So I’m feeling rusty, wordy, and mathematically stretched.

First, the Takeaways
With these caveats, I’m excited about the post. The following overview (sort of an elevator pitch) tells why:

1. The post was inspired by a Tweet and illustrates why I’m delighted with how Twitter has been enhancing my professional thinking.
2. The Tweet links to a problem from the NCTM August 2016 issue of Teaching Children Mathematics (TCM), one of those low-threshold-high-ceiling problems that I love to offer students. [For more suggestions and information about these sorts of problems, check out the NRICH site from the University of Cambridge and Jo Boaler’s youcubed site from Stanford University.]
3. When I tried the extension to the problem suggested in TCM, I found myself in a state of mathematical discomfort, a good reminder about what students often feel when facing new mathematical challenges.
4. I asked for mathematical help, another reminder of what I want to encourage students to do.
5. Working on the extension reminded me of the importance of always first solving any problem that I’m considering presenting to students
6. It’s important and often tricky pedagogically to decide when to tell or help, or when to leave a problem unresolved. So, if you want to think about the math by yourself, stop reading before you get to the end of the post.

Those are the takeaways I hope you’ll think about from reading this post.

The Tweet That Inspired
In mid-August, Mike Flynn (@MikeFlynn55) posted a problem on Twitter and asked for student work.

In order to contribute, I contacted Sara Liebert, who teaches at John Muir Elementary School in San Francisco. Last year Sara taught fourth grade; this year, she’s the school’s math coach but is also teaching fifth-grade math daily to the same class of students (with a few changes). I was fortunate to spend time in Sara’s class last year and collaborate with her to plan her math instruction, and I look forward to doing the same this year. I sent Mike’s tweet to Sara, and she presented The Cycling Shop problem to her fifth graders to work on in small groups.

After the students had time to work on the problem, Sara organized a gallery walk so that students could look at each other’s work. Below are two samples, which I sent to Mike. In the first, the students show the eight combinations they found. In the second, the students show ten combinations, with #9 incorrect, but the organization of their paper shows that they thought perhaps there could be more.

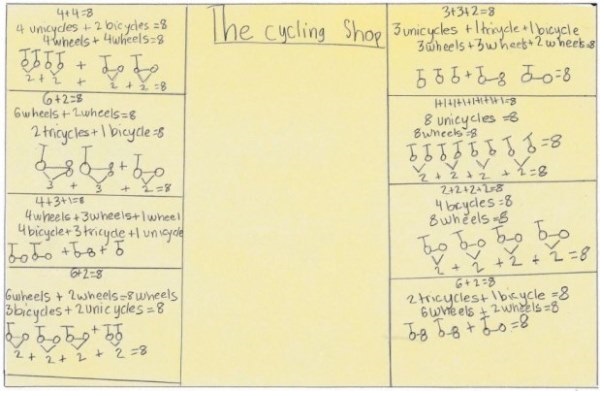
A Follow-Up Idea
Sara felt the experience was successful. The problem was accessible to the students, it pushed their thinking, and they enjoyed working on it. Sara asked me for a suggestion for a follow-up problem that she could put on the Math Menu, which she uses as a regular part of her instructional program. (For more information, you might be interested in “Using Math Menus,” an article I wrote for the October 2016 issue of Educational Leadership. The article includes some student work and photos from Sara’s class last year. The article is available online free of charge until November 1, 2016.)

The Teaching Children Mathematics article includes extensions, one of which is for students to explore combinations of unicycles, bicycles, and tricycles that could be built for other numbers of wheels. The suggestion is that they could look for patterns and begin to make generalizations about the possible combinations there are for each number of wheels. This seemed like a good follow-up.

Then I thought I’d better try the problem myself—always important, I’ve learned, before assigning a problem to students (as I mentioned above in Takeaway #5). I grabbed a piece of scratch paper, started to think, and kept notes. Here’s what I jotted down:

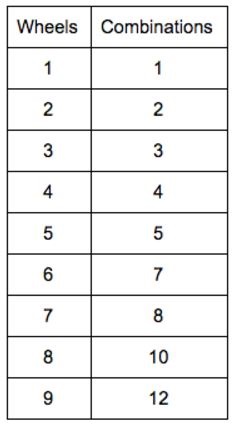
Now I was getting suspicious. When solving the original problem, I had found 10 possible combinations of unicycles, bicycles, and tricycles for 8 wheels, yet for 0, 1, 2, 3, 4, and 5 wheels, the number of possible combinations was equal to the number of wheels.

When I tried 6 wheels, I found that the pattern didn’t continue. I identified 7 possibilities—6U, 4U and 1B, 3U and 1T, 2U and 2B, 1U and 1B and 1T, 2T, and 3B.
For 7 wheels, I found 8 possibilities—7U, 5U and 1B, 4U and 1T, 3U and 2B, 2U and 1B and 1T, 1U and 3B, 1U and 2T, 2B and 1T.

What was going on here???

What Did I Do?
I felt mathematically stuck . . . and mathematically sort of lonely. Since I was away on vacation in upstate New York on a lake in the Adirondacks at a getaway accessible only by boat, I had no face-to-face access to math friends. But we do have internet service.

Who could I check with? Maybe Mike, since he suggested the problem? But I’ve never met Mike. Well, we’ve “met” on Twitter, but I felt a bit uneasy about sharing my mathematical confusion and airing my weakness. (Maybe this is what kids feel when we give them problems and they’re not sure of their thinking, as I suggested above in Takeaway #3.)

I decided to send my findings to both Sara and Mike, using email instead of Twitter because 140 characters simply weren’t going to do it. I confessed to Mike that it was an unsettling way to begin a correspondence beyond tweeting with my personal mathematical confusion. But, hey, I did it.

And I’m pleased I did. Mike responded and described his process of first simplifying the problem to just unicycles and bicycles. He included the drawings he made to help his thinking. He also included what he found for Unicycle/Bicycle/Tricycle combinations. Mike’s table was confirmation for me that I was on a similar mathematical track, and this was comforting.

I also sent a message for mathematical help to Henri Picciotto (@hpicciotto on Twitter, also check out his My Math Education Blog). This was easier for me to do since Henri and I know each other, meet face-to-face semi-regularly, and stay mathematically in touch. Henri wrote back to Michael, Sara, and me:

Henri’s message was a mathematical relief, offering hope that he could shed some light on the problem. But what I appreciated just as much was to learn that Henri had gone on a search for help, and also that he didn’t want to “spoil” the investigation for us if we preferred to keep struggling. As I wrote in the Takeaway #6 above, it’s an important and often tricky pedagogical decision about when to help, tell, or leave the problem be for students. The decision differs in different situations, and for different students, and always calls for a considered approach, which Henri did thoughtfully in his message.

We were eager for Henri’s help, and in his next message, he wrote:

Wow! I loved this. Not only did I love the simple visual representation that made a mathematical contribution to my thinking, I also loved seeing another example of how Cuisenaire rods can be a wonderful problem-solving tool. [About Cuisenaire rods: I’m always appreciative of the Tweets about Cuisenaire rods from @GlenysHanson and @SimonGregg and for Simon’s thoughts in his Following Learning blog.]

But There’s More!
Henri also included in his message a formula that he found on Wikipedia for figuring out the number of combinations for any number of wheels, which he claimed not to understand but that he found worked for the numbers of wheels that he tried:

round ((n + 3) ^ 2 / 12)

A formula that begins with “round”? Geez, another bit of mathematics that I’d never heard about before. Henri explained that “round” in the formula means to round to the nearest whole number. (Got it, but I’m still amazed to see it in a formula.)

I tried the formula, now happy that I had something to do. For 8 wheels, I had found 10 combinations. Using the formula with n = 8, I figured 8 plus 3 is 11, 11 squared is 121, 121 divided by 12 is 10.083… or 10 R1 (which is what I figured mentally and interpreted as 10 and a very little bit more), and that rounds to 10. Success! I tried it for 4 wheels to see if the formula produced 4 combinations: 4 plus 3 is 7, 7 squared is 49, 49 divided by 12 is just over 4, which rounds to 4. Success again!

Henri commented that the formula was mysterious. I agree.

At this point, I was as curious about what Henri had googled to get to the Wikipedia page as I was about the mathematics and the formula. I asked, now deciding there was no holding back. The first thing Henri did, he explained, was to enter the sequence of numbers (1, 2, 3, 4, 5, 7, 8, 10, 12—the numbers of combinations in Mike’s recording) into the search box of the Online Encyclopedia of Integer Sequences. Henri wrote that he “found that this particular sequence turns out to be relevant to lots and lots of problems.” And he went from there.

If you’ve gotten this far, I suggest that you reread the takeaways I included at the start. I think they’re an apt conclusion.

A Suggestion for a Different Follow-Up Problem
Back to the fifth graders: I noticed on their papers that students had found combinations for using 8 wheels that included building 0, 1, 2, 3, 4, 5, 6, and 8 unicycles. No group found a combination that included building 7 unicycles.

So . . . I’m thinking about presenting the students with my conjecture: With 8 wheels, it’s not possible to build 7 unicycles and use all of the wheels.

My Math Menu suggestion would be a writing assignment: Do you agree with my conjecture? Write an explanation for why you think my conjecture is true or why you think it’s false.

Stay tuned for how that goes—I haven’t tried it yet. Or let me know if you have another follow-up idea.