At a Math Solutions retreat, Nicholas Branca posed this for us to investigate:
If only two numbers are marked on a number line, is it possible to figure out where all numbers are located?
Nicholas had us try for a few pairs of numbers, to be sure we understood the problem. For example, we tried a few using zero for on of the two points—0 and 1 (easy, peasy), then 0 and 3 (OK to eyeball), then 0 and 11 (we reached for rulers). Then we tried a few where neither of the pair of numbers marked was zero—1 and 2 (again, easy peasy), 3 and 5 (also OK to eyeball), 8 and 20 (we used rulers again).
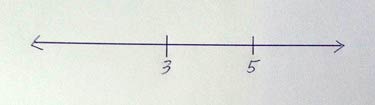
We investigated in small groups, drawing lines, marking a pair of points, assigning them numbers, and seeing if we could figure out where all of the other numbers would go. We discussed different strategies.
I can’t remember exactly what I did then, so I played around with the problem a bit this morning. Then I explored various pairs of numbers:
- consecutive numbers (e.g., 6 and 7, or 10 and 11)
- one number a multiple of the other (e.g., 5 and 20, or 5 and 50)
- numbers with a common factor (e.g., 8 and 12, or 9 and 12)
- relatively prime numbers (e.g., 3 and 14, or 2 and 7)
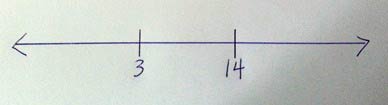
I began to think about numbers other than whole numbers. And then negative numbers.
I stopped to write this blog post.
Musing As I Wrote
It’s always tempting to procrastinate when writing. It’s especially easy at the computer. As I’ve confessed recently, I’m new to blogging and tweeting and have been doing some catching up this summer, which is an easy way to procrastinate and still feel productive. I recently read Dan Meyer’s blog post, The Three Acts of a Mathematical Story. (OK, OK, I realize that he posted this on May 11, 2011, but I’ve already confessed to being a newbie to blogs and tweets.) Although I began as a secondary math teacher, I’ve been absorbed with elementary school math for most of my career and I’m interested in ways to apply Dan’s thinking about secondary math teaching to the elementary level.
I actually learned about Dan’s thoughts about three-act math from its application in a Kindergarten lesson that Joe Schwartz posted on his blog two months ago, Nobody Puts Kindergarten in the Corner! Joe got the lesson idea from Shark Bait, a post on Graham Fletcher’s blog.
I was especially curious about Joe’s post because Kindergarten teaching isn’t my thing. Ann Carlyle, who recently wrote a book with Brenda Mercado, Teaching Preschool and Kindergarten Math, once described Kindergarten to me as “every day is a birthday party.” That scared me off. But Ann and Brenda’s book (yes, books are still an important part of my professional learning) and wonderful accompanying videos made me think about reconsidering my attitude toward working with children this young.
Back to three acts and my morning thinking about number lines. Maybe Nicholas’s problem can be thought of as a three-act math investigation.
A Number Line Exploration in Three Acts
Act One
From Dan: “Introduce the central conflict of your story/task clearly, visually, viscerally, using as few words as possible.”
From me: Draw on the board a horizontal line with two marks. Explain: This is the start of a number line. So far I’ve made marks for two whole numbers. Now I’m trying to figure out how to make marks for all other whole numbers. Is this possible to do, no matter what two numbers I use to label these marks?
Do a few examples, as Nicholas did? Or not? (I think I would.)
Then explain: Try with other pairs of numbers. Find numbers for which it’s not possible to create the entire number line, or make a convincing argument for why it’s possible to do so with any two whole numbers.
Act Two
From Dan: “The protagonist/student overcomes obstacles, looks for resources, and develops new tools.”
From me: Students work in pairs or small groups exploring pairs of numbers of their choosing.
Act Three
From Dan: “Resolve the conflict and set up a sequel/extension.”
From me: Discuss as a class. If students have found pairs of numbers for which they think it’s impossible to create a number line, maybe give time over a day or two for others to investigate. If students have arguments for why it’s possible for them to create a number line from any two points, have them write their arguments on posters for the class to analyze.


(Where you write: “Do a few examples…? Or not?” At least initially: I probably would not.)
I have taught using variations of this activity in the past (usually without negative numbers; sometimes returning from the whole numbers later to the positive fractions). Depending on the student(s), some additional considerations are:
[1] If only one number is marked on the number line, then can we figure out where all numbers are located?
(I think I prefer the more open-ended question of, how many number labels do you need to turn a line into a number line? What’s the difference between a line and a number line, anyway? And what are the key properties of a number line?)
One way to broach [1] is to have different students work with the same initial line with just a single number marked. A key concept that I would hope to elucidate in this process would concern when two number lines are equivalent: namely, if you position the two number lines so that a particular number from each of them lines up, then all the number places from each of them must line up. Sometimes I investigate this by drawing number lines above and below one another; you could use transparencies or other approaches to superimpose. (This is also an idea that carries over well, later on, when talking about equivalence of fractions.)
[2] Once you have established that a line with 1 number marked can be made into a number line (but not uniquely) and a line with 2 numbers marked can be made into a number line (uniquely) what about a line with 3 numbers marked?
In particular, is it possible that a line with three numbers marked (assuming always that they increase when moving from left to right – another key concept) does not correspond to any number line?
For example: You could show a line in which 3 and 4 are very close together, and 5 is very far away. Could this correspond to a number line? This turns out to be a good one-on-one clinical interview topic, too. (As I’m sure you know, young children label number lines in idiosyncratic ways! I’ve often thought it might be interesting to return and have current/prospective teachers try to label a number line that is logarithmic in scale…)
[3] Which pairs of numbers are easier to work with? Why? What are some strategies that emerge when carrying out this task?
An example of a high-level strategy is to try and find 0 and 1. (The key point of establishing the “unit” or “unit of measurement” — more of the foundational work for fractions.) Depending on the goal, though, this might not be necessary; for example, if you show students 7 and 15, and ask them to find the location of 13, then the 0 and 1 benchmarks may not play much of a [direct] role at all.
You mentioned picking relatively prime numbers; indeed, 7 and 15 are relatively prime. But they are not as tough to work with as, say, your example of 3 and 14. In the case of 7 and 15, the difference of 8 means that bisecting three times can lead to some good labeling! (How do students come to see “bisecting” as a good strategy with a difference of 8? Is it a good strategy with a difference of 9, e.g., if given 7 and 16 and asked to find 13? Lots more to say, but I’ll cut off here.)
MQ
https://mathwater.wordpress.com/
Thanks for the thoughtful and detailed comment — gives me much to think about.
A question: With what grade level students have you done this? Any tips? Thanks in advance.
RE: Grade level
For the activities outlined above- Grades 17/18 (graduate students in elementary education). Do the same (or similar) activities work with younger students? I believe so; but the pace would be fairly different. (For example: My repeated remarks around fractions are because I return to the number line just a couple of months later, and we apply the ideas developed with whole numbers to the fractions. We also talk about how the number lines for whole numbers and fractions are similar/different…)
RE: “Any tips”
There are more recent ways number lines have been explored using computer-based technology, but I think a good couple of activities are described here:
Petitto, A. L. (1990). Development of numberline and measurement concepts. Cognition and Instruction, 7(1), 55-78. Retrieved from http://lchc.ucsd.edu/Festschrift/Library/Numberline-n-Measurement.pdf.
The article discusses two sequential experiments involving students in grades 1 through 3. I quite like the latter task, in which students (who have already completed a number line task) are shown different rulers (only one of which has numbers spaced with equal-sized intervals) and asked which one they would choose to help solve “numberline [sic] problems.”
The equal-spacing notions (which go back at least to the work of Piaget) are related to the extension problem [2] suggested in my earlier comment.
If I were teaching this to younger children (much younger than “Grade 17/18”!) then I might start by reviewing the number line (perhaps with a few tick marks that are unlabelled); then present a number line with tick marks, and just two numbers labelled (can they label the missing numbers? yes- counting tick marks suffices); and then present a number line with two labelled tick marks, but without any other tick marks or numbers (now we have the original task). For the pair of numbers, I might choose a couple like 3 and 5, and ask the students if it is possible to locate any other numbers using what we have.
I would be inclined to let the discussion evolve organically from there, but in my mind I’d want the key points to be: numbers get bigger as we head east, and smaller as we head west (and so 4 is certainly between the 3 and 5- a parenthetical remark that can be unpacked at length); the intervals should be of the same size (and so 4 is exactly halfway between the 3 and 5: with a suitably long number line, you could draw the 4 far too close to the 3, and see if anyone objects- this is a subtle point, though, because 1st grade students may have a pretty good handle on the order of the counting numbers, but the “halfway between” notion requires a bit of proportional reasoning perhaps not yet accessed); and knowing the size of a “unit” lets us find all the numbers (and so once we have placed 4 in its rightful spot, we can use the distance from 3 to 4 as our unit, and count backwards to 0, or forwards to our marked 5… and beyond!).
MQ
This has me thinking about exploring with students the whole idea of “different number lines.” If I make two different number lines with different scales, is one “right” and the other “wrong?” Why not? When would one be better than the other?
Marilyn Burns + Dan Meyer = Mathematical Gold
This problem of dividing a number line is similar to what we teach in my school district, only it is based on the native way of understanding measuring. Jerry Lipka, who recently retired from the University of Alaska Fairbanks, and Dora Andrew-Ihrke, a retired Yupik teacher, developed math concepts based on the Yupik way of halving. Dora is an amazing teacher who shows students how to fold paper strips into equal fractions from half to twelves. There is so much we can learn from each other. Math is exciting when you can look at it from different angles.
This is a fun problem for Geometry students equipped with compasses. And when they resolve the initial question, asking them which real numbers they can find is such a wonderfully rich follow-up!
Do you discuss units at all, and if so, how? As presented, my concern is that it’s continuing a trend of abstracting away from numbers as representatives of real world things; in the case of a number line, a unit is a measurement of length. Obviously, that measurement itself is arbitrary, and a randomly drawn number line will likely not have a standard unit as its scale length. But even if the distance between 3 and 5 is, say, 4.5 cm, then the unit scale of that number line is 2.25 cm… which is still an acceptable unit scale. But without discussing units at all, I’m wary that we’re just reinforcing that the number line is a bunch of numbers arbitrarily-but-equidistantly distributed on a line. Is that the sole purpose of a number line?
Whole numbers, yet, too. Obviously, the exercise needs to be age appropriate, but for older students how about 4.2 and 5.6? 3 1/7 and 25 4/9? Pi and Phi?
Thanks for your thoughts. They give me much to think about. Now I need to get into classes at different levels and explore with the students. Stay tuned.
As per Patrick’s suggestion and without giving away a general solution, let me just say that I tested this number line activity with a compass and a straight edge and I can construct the points in between any two rational values, although it is much simpler when using integers and much easier to read.
As for irrational numbers, well, those are a different kettle of fish. 🙂
Just reading the question by itself, I jumped to the conclusion that, no, you cannot tell where all the others numbers are because you don’t know what the scale is.” It could be logarithmic and, if so, we don’t know what the base is (e.g., base 10, base 2, natural log, etc.) However, if you assume the scale is constant and linear then, yes, you can simply extend the axes as much as you like.