Here’s what Amber did to add 1/2 + 2/3:
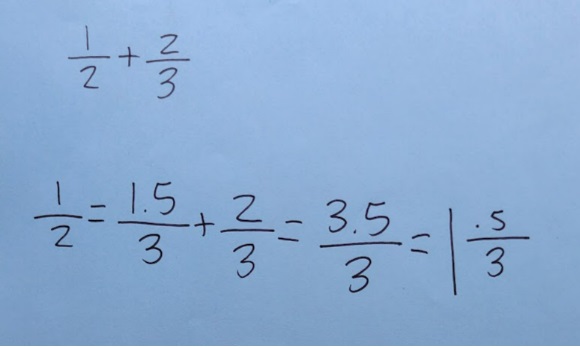
This is a solution that I’ve never seen before . . . or since.
I was interested in engaging a class of fifth graders with Amber’s solution and learn about how they would make sense of it.
A Pedagogical Note
I was aware of the error in Amber’s work. While it’s correct, though not conventional, to write 1/2 = 1.5/3, it’s not correct to write 1/2 = 1.5/3 + 2/3, which is the second part of the equation she wrote. I’ve found that this type of error isn’t unusual when students record as they think, but I chose not to discuss this at the time, or to alter Amber’s work. If a student had brought it up, I would have explained.
How I Began the Lesson
My plan was to formulate some conjectures for the students to consider as a way for them to think about Amber’s work. To begin, I wrote Conjecture on the board. The students weren’t familiar with this word and I asked them to turn and talk about what they thought it might mean. Students focused on different parts of the word to try and figure out its meaning. Several felt that “ject” meant something was being pushed forward or pushed out. Others felt that “con” had something about bringing together or with other things. One pair looked it up in the dictionary but found the definition too wordy and not useful.
I then gave them a brief definition, that a conjecture in math was an idea that you thought might be true but you weren’t absolutely sure. I then told them, “I’m going to make a conjecture that I think is true, and I wonder if you agree and if you can think of a way to prove it.”
My First Conjecture
I wrote my first conjecture on the board and again had them turn and talk. I said, “Decide if you agree with me that it’s true, and come up with a reason to explain why.”

The first student gave an explanation that made sense to others in the class. He said, “I know that 1/2 + 1/2 equals 1, and I know that 2/3 is more than 1/2, so the answer has to be more than 1.” Another student presented a different idea, “I figured out the answer, so I know it’s more than 1.” She went on to explain, “I changed both fractions to sixths and added 3/6 plus 4/6 and I got 7/6, and that’s 1 1/6.” I asked others to share as well, even if they had the same or similar ideas as those already shared.
There are still some students who struggle with adding fractions with unlike denominators. I projected Amber’s work and modeled using fraction tiles to add 1/2 + 2/3. The tiles were also available for students to use as needed.

After I placed the 1/6 tile, a student suggested that I could have used two 1/12 tiles instead, so I did that as well.
My Second Conjecture
Next, I wrote this equation on the board and again asked them to turn and talk.

Some students were sure that it was true because half of 3 is 1 ½. Others agreed, but some were surprised and unsure. Many were curious to see a fraction in the numerator of a fraction.
“Are you allowed to put a fraction in a fraction like that?” one boy asked.
I responded, “It may seem unusual to have a fraction in the numerator of a fraction, but it’s mathematically OK. What’s important is that you can explain what it means. Actually, fractions like these have a name—they’re called complex fractions.” I wrote that on the board.
My Third Conjecture
This was the last conjecture I planned to present. This was easier for them. They could relate it to the previous conjecture because they knew that .5 was equivalent to 1/2. Still, some were a bit surprised and wanted to know if you could put a decimal in a fraction.

How the Students Read 1.5/3
I posted Amber’s work on BlueSky a few days ago, before I taught this lesson, and this is one of the responses I received.
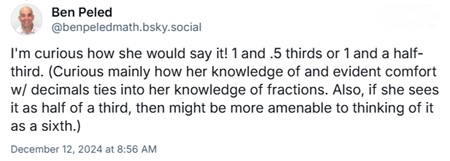
Because of this post, I asked the students about how they would read the fraction. (Thanks, Ben, for the suggestion.)

I recorded how the students reported they would read the fraction 1.5/3.
After I wrote the last suggestion, 1 point 5 divided by 3, a student asked, “Isn’t division the same as fractions?” I responded, “So you’ve just made your own conjecture: Division is the same as fractions. That will be interesting for us to discuss.”
A Pedagogical Note
The relationship between division and fractions is an important mathematical idea, but it wasn’t an idea I wanted to follow up on at this time. Instead, I wanted to get to a writing assignment where students would write about Amber’s work. I chose to acknowledge his contribution and definitely will return to it. Making choices in the flow of instruction is never easy.
The Writing Assignment
I explained, “I’m interested in how you would explain how Amber reasoned, and I’d like you to write about your thinking.” A student asked if they could explain how they did the addition. I told them it was fine to include their own reasoning, as long as they also explained how Amber reasoned. Here’s a PDF of the worksheet I prepared for the assignment.

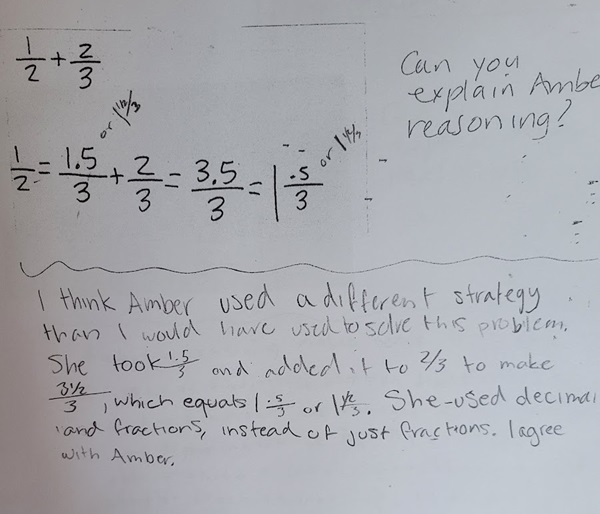
He agreed with Amber but wrote that he would have used a different strategy.

She first explained how she would solve the problem and then explained Amber’s reasoning.
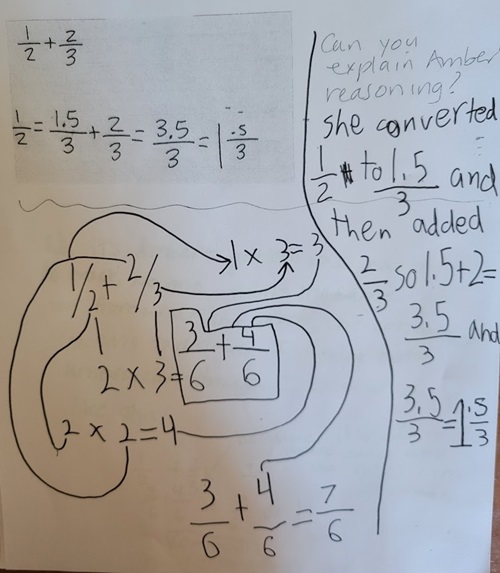
He showed in detail how he figured out the answer of 7/6 and also explained how Amber reasoned.

This was one of the more detailed explanations of Amber’s reasoning.
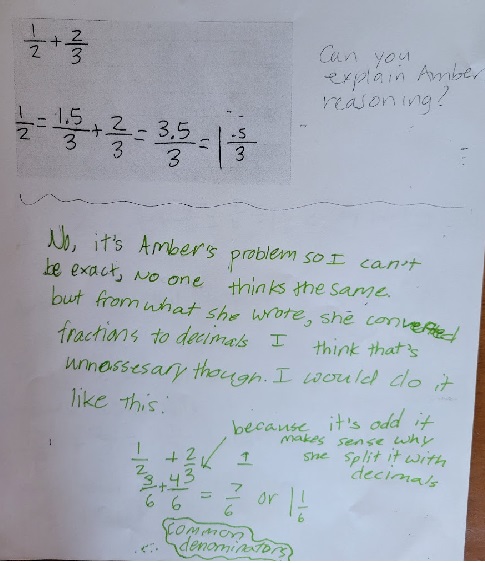
She expressed that she couldn’t really be “exact” about Amber’s reasoning and focused her paper more on what she would do.

He described both Amber’s thinking and his method.
A Final Comment
I had been mulling over how to present Amber’s solution to the class, and then was inspired from attending a webinar given by Susan Jo Russell and Deborah Shifter that focused on engaging students in formulating and discussing conjectures. It was mathematically thrilling. The webinar was part of the TERC Speaker Series offered by their Forum for Equity in Elementary Mathematics. Free to all, this was the second in a series of five webinars. For information: https://www.terc.edu/mathequityforum/news/speaker-series-announced/

It does make sense that it wasn’t time to address the “writing it out as you think” issue 😉 I hope there was some comprehension of halfness as opposed to “I know how to add decimals so I’ll do that!” and I’m glad folks could sort through it being “half of a third, oh, let’s figure that out!”