This is the third blog I’ve written about the same division problem―100 ÷ 3. After the first blog, the problem still tugged at me. Just about a year later, I wrote the second blog, and then I was sure that I was done thinking about this problem. Not so. When recently interviewing fifth graders about division, I heard two answers from students that I’d never heard before. The students’ answers gave me the impetus to create and teach this lesson.
First, a Look at a Student Solving 100 ÷ 3 Correctly
When Nishi interviewed Santos, he explained how he reasoned to get the answer of 33 R1. He used multiplication to figure, demonstrating his ability to apply the inverse relationship between multiplication and division. Take a look. (Learn more about the interviews at the end of the blog.)
What Were the Answers I’d Never Heard Before?
In my recent interviews with fifth graders, the two answers that I had never heard before were 30 R10 and 25 R25. Both of these answers are mathematically viable, but they aren’t the answer we want kids to give for solving this numerical problem without a context.
More detail: Of the 20 students in the class, 11 students answered correctly (all 33 R1) and many reasoned similar to the way Santos explained. (When interviewing, we always ask students to explain how they reasoned, whether their answer is correct or incorrect.) The other nine students either answered incorrectly or didn’t answer at all. Five students came up with 30 r10 initially, but two of them switched their answer to 33 R1 as they explained. (The incorrect answers that other students gave included 90 R10, 35 R2, and 33.) I also learned from the interviews that most students in the class, all but two, demonstrated solving contextual problems that involved multiplication and division. How could I leverage their mathematical strength and plan instruction to help all students think about solving a numerical problem like 100 ÷ 3?
From listening to students reason, I felt that I had valuable marching orders for planning instruction.
A Pedagogical Note: I’ve read and thought a good deal about the value of strength-based teaching rather than focusing instruction on filling gaps and fixing misconceptions. Yes, I’m aware of learning gaps in the class. But it makes sense to me that instruction builds on what students know to help them develop, cement, and extend their understanding and skills. In the spirit of teaching from students’ strengths, I chose to present 100 ÷ 3 in a context.
The Lesson I Taught
Here’s what I did. I began by telling the students a story that led to thinking about 100 ÷ 3.
Mr. B’s Three-Wheeler company makes tricycles.
They can make 5 tricycles each day.
He received a shipment of 100 wheels.
How many tricycles can Mr. B make with the 100 wheels?
I then said, “I’m not interested yet in the answer to the question. First, I’d like to know what math problem we need to solve to answer the question about how many tricycles Mr. B can make.” There was agreement that the problem to solve was 100 ÷ 3.
I wrote 100 ÷ 3 on the board and then wrote Day 1 underneath. My plan was to create a table that would capture how many tricycles Mr. B made on Day 1, Day 2, and so on, until he used all 100 wheels.
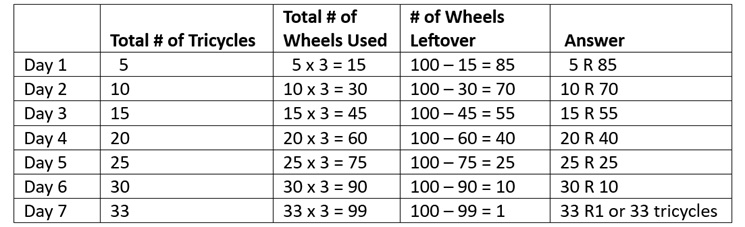
This is the finished table I had in mind.
I had four questions that I would ask to complete each row on the chart:
- How many tricycles were made from the 100 wheels at the end of the day?
- How many of the 100 wheels were used at the end of the day?
- How many wheels were still leftover at the end of the day?
- What’s the answer to the division problem at the end of the day?
I began with Day 1 and the students answered the four questions:
- Five tricycles were made at the end of the first day
- He used 15 wheels because 5 x 3 = 15. (I recorded 5 x 3 = 15 to emphasize the connection between multiplication and division.)
- There were 85 wheels leftover. (Here I recorded 100 – 15 = 85.)
- The answer to 100 ÷ 3 at the end of Day 1 is 5 R85, which means they made 5 tricycles with 85 wheels remaining.

Here’s how I recorded for Day 1.
So far, so good. I then wrote Day 2 under Day 1 and repeated the questions, again recording. I continued in this way through Day 6 after which they had made 30 tricycles and still had 10 wheels remaining.

This is how I recorded for the rest of the chart.
The discussion about Day 7 was interesting. Students had several ideas. “They don’t have enough wheels to make five tricycles.” “They should have ordered more wheels.” “They can only make three more tricycles.”
I asked, “What would I write in the last column? What’s the answer to how many tricycles he made at the end of Day 7?” The agreement was that the best Mr. B could do on Day 7 is to make three more tricycles, which would bring the total to 33 tricycles with 1 wheel left over. I don’t show the answer on this board.
A pedagogical note: I don’t know why I didn’t fill in the row on the board for Day 7. Honestly, I think my board work is a little sloppy. In my defense, this was the first time I had taught this lesson and at the time I was also thinking about what I’d do next. It’s hard to teach and think at the same time.
Revising the Question
I then changed the question. I said to the class, “All of the answers in the last column are possible answers for the question about how many tricycles Mr. B can make. But supposed I changed the question to this: What is the greatest number of tricycles he can make with 100 wheels?” (I emphasized “greatest” as I said this.)
I asked them to turn and talk and then had several share their thinking. Two ideas emerged. Some said that the answer would be 33 remainder 1. Others said that you don’t need the remainder. One student explained, “You could just say 33, because that’s the greatest number of tricycles he could make with 100 wheels.”
I pointed to all of the other answers on the chart. “What about these answers?” I asked. The agreement was that they were OK for the first question, but not if you were trying to figure out the greatest number of tricycles. Some students seemed intrigued that a problem could have more than one possible answer.
Referring Back to the Interview Question
I then reminded them about the interviews about division that we had done the week before. I pointed to the problem on the board—100 ÷ 3—and told them that they had answered this question, but without the story about Mr. B and the tricycles. I said, “I’ve interviewed many, many students, and I was very interested to hear answers from some of you in the interview that I’ve never heard before from students.” I went on to tell them that five of them gave the answer of 30 R10 (and I circled that on the table) but three of the five changed their answer to 33 R1 when they explained how they reasoned. I told them that one student gave 25 R25 (and I circled that on the table) and stuck with that answer.
My Closing Remark to The Class
For better or worse, and with some trepidation, here’s what I said next, “I agree that the answers that I’ve never heard before in interviews, and the other answers on the table, are all mathematically possible for the question about how many tricycles Mr. B could make with 100 wheels. But, if you are solving the math problem 100 ÷ 3 and there’s no story attached, like the problem you were given during the interview, then you need to give the answer after you’ve done all the dividing you can, and that’s 33 remainder 1.” There were some murmurs and some grumbling.
One boy asked, “Could you give the answer of 33 and one third?” I responded, “Yes, because that shows you did all of the dividing possible.”
Another asked, “What about 33.3333333 and so on?” I responded as I did for 33 1/3.
One girl asked, sort of indignantly, “Who made that rule?”
I ended the lesson at that time, even though there was mathematical discontent from some of the students. Honestly, I had no further explanation to offer . . . at that time.
A Pedagogical Note: I wasn’t comfortable with the “rule” I gave the students about having to do all the division possible. It felt like a “just because” rule that I wasn’t able to explain. I’ve had this experience before, feeling at a loss to help students understand an idea. If the idea is rooted in social knowledge, like how we write the symbol for plus or equals, or how we write exponents as tiny numerals, then I’m comfortable with telling them the convention. The source of their understanding is external to them and teaching by telling makes sense. But here I was thinking that there must be a logical reason why we accept 33 R1 but not 30 R10 or 25 R25 as the correct answer to 100 ÷ 3. That said, I didn’t have access at that time to how to help them make sense of a reason why. Since then, I’ve dug in and am working on another blog about just this issue. Stay tuned.
The Students’ Written Reflections
I asked the students’ regular teacher, Aimee Levin, if she would have them write about this experience the next day, after they had time for their thinking to marinate.
A pedagogical note: In a class discussion, I learn only about how the students who speak are thinking. That’s why I find it important, even essential, to have students write. And I’ve learned that a little distance from an experience often helps students’ thinking settle and makes it easier for them to reflect.

This is from the student who seemed indignant about the division rule.

He referred to the “normal” answers for 100 ÷ 3.

She learned that the same numerical problem can have different answers for different contexts.

He wrote about learning two things with division—how to use a table and how to use multiplication to help solve a division problem.

She focused on the different possible answers for 100 ÷ 3 and also included a problem of her own about sharing cookies.

This student was also interested in different possible answers to division problems.
The Two Previous Blogs About 100 ÷3
I wrote my first blog about this problem in early 2020, What Was Jonah Thinking? This blog includes a video of me interviewing Jonah who solved the problem and gave the answer of 33¼. I showed the video to fifth graders, had them write letters to Jonah, and included some of their letters in the blog.
A little more than a year later, I wrote another blog, What Is 100 ÷ 3? Why We Ask and What We Learn. This blog also includes a video, this time of Mallika Scott interviewing Zaynab solving the problem. Zaynab began by adding 25 + 25 + 25 and commenting, “Each of them got 25.” She was referring to a problem the class had solved about sharing a pack of 100 Origami papers among three classes. Zaynab knew that she had 25 papers left and then continued to figure out how to divide 25 into 3 shares. This helped me think about how contexts can be useful for helping students develop the operation sense they need to tackle numerical problems.
It was wonderful to have these videos to view multiple times. (I wish I had videos of the fifth graders giving the answers of 30 R10 and 25 R25.)
More About the Listening to Learn Interviews with Students
All teachers in the district where I taught this lesson use Listening to Learn (LTL) math interviews to learn about their students’ numerical reasoning. What is 100 ÷ 3? is included in Interview 8 of the ten Listening to Learn interviews. As with all of the interview questions, we’re interested in learning about the numerical reasoning strategies that students access when solving problems. We ask students to solve all problems mentally without pencil and paper. The interviews are organized into four areas—Foundations of Numerical Reasoning, Addition & Subtraction, Multiplication & Division, and Fractions & Decimals.
Listening to Learn generates both individual and class reports. For this class, I learned that half of the students applied the inverse relationship between multiplication and division when solving division problems, and I wanted to address this important idea as well. That’s why I was explicit about including multiplication in the table we filled in about Mr. B’s tricycles.
If you’re not familiar with LTL interviews, you can access an overview here and learn about the specific reasoning strategies we assess.
Thanks to Colleagues for Their Help
It’s hard for me to think by myself when planning lessons and reflecting on them. Thanks to Leo Kostelnik for coming to class, observing the lesson, and then spending a valuable hour talking with me about what had occurred and what we had learned. Thanks to Phil Daro for reviewing the students’ written reflections and talking with me about the essentials of division. Thanks to Jenna Laib and Lynne Zolli for helping me prepare the lesson. Thanks to Aimee Levin for allowing me to “borrow” her class and help with interviewing the students.

