I struggle with how to teach topics that revert to learning procedures, too often without understanding. Take adding decimals. This is typically part of grade 5 math instruction. But every time I’ve given students the reminder to line up the decimal points and then add, I’m reminded of the fraction counterpart: Yours is not to question why; just invert and multiply. My ongoing search is for ways to engage students with adding decimals in a way that promotes making sense, reasoning numerically, and solving problems, not merely learning a procedure.
I chat from time to time with Nina Sudnick, a teacher at West Elementary in Athens, Ohio, now teaching math to one class of fourth graders and two classes of fifth graders. When Nina and I talk, usually on weekends, we often brainstorm ideas for lessons. Nina is currently working on decimals with her fifth graders. She’s been using ideas from Teaching Arithmetic, Lessons for Decimals and Percents, Grades 5–6, a Math Solutions resource that I wrote with Carrie De Francisco. Nina described to me her recent experience from the book engaging students with The Lobster Problem. This is one of my favorite decimal problem-solving lessons that you can download from the Math Solutions website.
But when we’ve given students practice with adding decimals out of contexts, we’ve both found ourselves reverting to reminding students about lining up the decimal points before adding. And we agreed that this seems to put focus more on the procedure than on understanding.
As Nina and I talked, I recalled an idea. I can’t remember what sparked it and I’ve searched unsuccessfully for its source. (Please let me know if you have a source.) I offered Nina this instructional suggestion:
Write this on the board:
123 + 47 + 9 = 179
(Yes, I know I promised a lesson about adding decimals, but it’s always a good idea to start with something students are familiar with, here adding whole numbers.)
Ask: Is 179 a reasonable answer for adding 123 plus 47 plus 9? How could you explain without adding the three numbers?
(Actually, I asked Nina to write the equation horizontally on paper, since we were on the telephone. I told her I wrote the problem horizontally purposefully to avoid triggering the “line up the decimal point” algorithm and for leading into my next question.)
Discuss: I’d have students think first by themselves, then talk in pairs, and then I’d ask some to report to the class. Then, perhaps, I’d have them verify that 179 is, indeed, the correct answer.
Underneath the equation, write another on the board:
123 + 47 + 9 = 2.60
Ask: Suppose I had written this on the board instead and asked the same question: Is 2.60 a reasonable answer for adding 123 plus 47 plus 9? How would you explain?
(I meant for this to be a sort of silly question and I’d press for explanations. What would you answer?)
Discuss: Again, I’d use the Think-Pair-Share routine.
Present a problem: Suppose I told you that the second equation used to be correct before someone erased the decimal points that were in the addends. Can you figure out where to insert decimal points so that the sum of the three addends would actually be 2.60?
(How would you do this? How do you think your students would decide?)
Discuss: Again, I’d use the Think-Pair-Share routine.
(If I thought it was necessary, I might present another “missing decimal points” example to determine if this sort of problem was accessible to them.)
Explain how I created the puzzle: Then I might show the class how I created the puzzle, choosing three numbers first and adding them. Maybe I’d show this on the board:
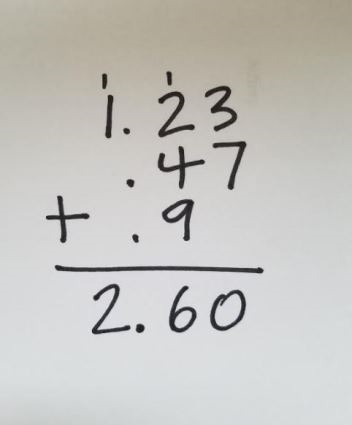
Then I’d explain that I wrote the problem horizontally, intentionally leaving off the decimals points in the addends to make the math puzzle.
Give an assignment: Now you’ll create an adding decimal puzzle the way I did. Your puzzle can have two or three addends. Follow these directions:
- Select two or three decimal numbers and add them.
- Write an equation for your problem, but leave out decimal points in the addends. (Your answer may or may not have a decimal point. If it does, be sure to include it.)
- Check your puzzle with a partner. (Hmmm, maybe I’d have students create their puzzles in pairs. This might be better for avoiding computation errors.)
- When your puzzle is ready, ask me to check it. (Check that their sum is correct and that they wrote the equation without decimal points in the addends. Then give them a blank index card.)
- On an index card, write your name(s) and your horizontal equation.
- If there’s extra time, make up another problem.
Keep the students’ papers, since they have the solutions on them. When all students have made at least one puzzle card, collect them, shuffle them, and distribute them to students (or partners) to solve. If you have a Math Menu, add this to the options. (For information about Math Menus, check a previous blog I wrote.)
I’d give time for them to complete this. And, even though I often feel the pressure of time when teaching, I’d stop myself from “moving on” and devote at least the next class to having students solve each other’s puzzles. Too often, I don’t give students enough time to explore, worrying that it’s too much playing. But Joe Schwartz’s recent blog, Play On, was an important reminder to me not to cave to the tyranny of time and allow students time to experience.
Possible questions for students, after they’ve had time to play:
- If you had to rank a puzzle as Easy, Medium, Hard (1 star, 2 stars, 3 stars), how would you decide?
- What makes a puzzle easy or hard? (Maybe have them create puzzles that are intentionally really easy or really hard.)

I will be teaching decimals to my fourth graders soon in an accelerated plan where they are actually taught fifth grade standards and will use these ideas. Thank you for the ideas
I love these! I have used similar puzzles with students ranging from grades 2 through 7. (Clearly, the 2nd graders didn’t get decimal versions…) I first saw this with decimals in Van de Walle — possible source? — and then I adapted it further from puzzles by Naoki Inaba.
I wrote about two early lessons here:
One was with an “intervention” group of 3rd grade students working on addition. The second lesson was with a class of highly motivated 6th grade students.
Later, I introduced the decimal puzzles to more kids: whole numbers to some 2nd graders, using language about “changing the place value” instead of multiplying by x. “You can make 5 into 5 ones or 5 tens or 5 hundreds…”
Then, I worked with a 5th grade class, using what I had learned from the other students. We warmed up with a few of the more challenging whole number problems.
“Make the equation true. The only catch is that you can only change a digit by multiplying it by a power of 10: 10, 100, etc.” This connects up nicely to 5th grade thinking about place value shifts.
Students used white boards on the rug, and shared their work in pairs/triads. We kept the discussion brief. I was looking to illuminate some thinking about reasonableness and estimation.
Then we launched into one with a decimal sum with a quick notice/wonder.
“This one has a decimal in the answer.”
“Wait, but how does that work if you can only multiply by 10 or 100 or something?”
“Do we have to divide?”
And they were off. I launched it with division, but kids swiftly started talking about it in different ways:
– moving the decimal (sigh, of course)
– making the digit into tenths, or hundredths, etc (“It says 9 but I want 9 tenths)
– multiplying by 0.1, 0.01, etc.
– multiplying by 1/10, 1/100, etc.
– lining up the digits (they had already seen it outside of school…)
– using logic (“I an’t turn the 5 into tenths because the sum will already be too big”)
I think using the “change by multiplying” and “change into __ ones, tenths, etc” language helped the students focus on the value and less on an algorithm they may or may not know. (…but it’s just a theory, since it’s not as if I had a control group!)
Like you suggested, I had some kids create their own. I gave examples on the blog. The students often created very complicated ones that taxed the working memory, and then we discussed how some that “looked simple” but involved a lot of regrouping/numbers that summed to a place value were actually harder. Like
2.9 + 13 + 0.8 = 1,300,000.0829
Is actually relatively easy, because you can “see” where the digits need to be, and then determine the place value from there.
78 + 122 + 409 + 31 = 46
Is actually much harder because it involves some numbers that paired together nicely (0.78 + 1.22 = 2, even, which means you can’t see the 78 or 22 anywhere in the final answer) and because students couldn’t decide whether to make the 409 into 40.9 or leave the 31 as 31.
(The solution is 0.78 + 1.22 + 40.9 + 3.1 = 46)
Based on Inaba’s work, I had actually designed the packets to get increasingly more challenging with each page — starting with only dividing by 10 without regrouping, then only dividing by 100 without regrouping, etc. moving onto ones that involved regrouping, ones that involve pairs of 1 or 0.1, etc.
I like that you started with reasonableness! Whatever you use as the launch is the lens that students will often use throughout their investigation — whether it’s reasonableness, or place value, etc. I knew I wanted to center my closing discussion on noticings about place value to address those 5th and 6th grade PV standards. If I were doing it for decimal addition, like you, I think it makes sense to launch it using reasonableness because that’s an excellent anchor for reasoning about an operation. These puzzles have so much potential!
Thanks again for sharing, Marilyn!
Thanks so much, Jenna, for your detailed comment. You’ve given me lots to think about and I look forward to getting into classrooms and seeing what happens. Your suggestions will truly help.
Thanks! This is great.
Thanks so much for this blog and all of your other meta-cognitive blogs which help us get inside your math mind and help us to nurture and develop our own math minds. I will try this with my pre-service teachers.
We finally went back to school today and we got to try out the decimal lesson you created last weekend. It went pretty much as you described in the blog. We talked about 127 + 43 + 9 = 179. We estimated then talked about why the answer was reasonable. Many students had trouble just estimating mostly because my wait time was too long and they just solved it. After pair sharing and sharing as a whole group we shifted to the next problem 127 + 43 + 9 = 2.60. I asked them if they thought this equation was true. Most of the students laughed out loud so I had them pair-share with their neighbor as to why that was so funny. When I called the class back together I heard various comments like: “Well, the single digit 9 is already bigger than 2.60”; “It’s impossible because the first addend is in the hundreds.” “There are no decimals in the problem so how could their be decimals in the answer.”; “If the first problem equals 179 how can the 2nd problem, with the same numbers, be equal to 2.60? It can’t!”. Moving along I said to them, “What if I told you the second problem was true but that someone had erased the decimal points in the addends…do you think it could be true? Spend some math-by-myself time to write down the second problem and see if you can insert decimals into some or all of the addends to make the equation true.” A few students asked questions about moving the digits around or changing it into a subtraction problem. One student asked about inserting zeros. I reminded them the problem needed to solved as written but that they could insert decimals and zeros. The vast majority of them eagerly went to work The students for whom decimals are a challenge were thinking and processing a bii longer but everyone tried something. As they finished their work they were invited to come to the carpet and quietly discuss their strategies with 1-2 students while other students finished their quiet thinking. (This is a routine we do often so they know to talk quietly and not to just say, “Here is my answer… .”) When everyone was finished, or almost everyone, we gathered as a whole group to discuss strategies. The majority of the students started by placing a decimal in the first addend to create 1.27. They shared that they knew they needed at least 2 so this was a good place to start. From there they either tried to figure out how much more they needed to make 2.60 and one student even subtracted 1.27 from 2.60 to find the difference (already subtracting by making sense of the problem.) One student talked about how she had inserted zeros to create the number 0.09 but she determined that this would not work because she did not want a 9 in the hundredths place. “Jason” said he started with the 43 and the 9 and made .43 and .9 which equals 1.33 and then he just added on the 1.27 because he could see he just need something around a one. At the end of the discussion “Frank” said he found a sum of 1.79 by adding 1.27 + .43 + .9 and he wasn’t sure what went wrong. I asked what place value the 9 was in and he said tenths. I then said, “Well, I wonder how it ended up in the hundredths place?” The expression on his face indicated he may see what happened but I will follow-up with him later. He is understanding of decimal place value is still a little fragile and/or inconsistent, which is typical of 4th and 5th graders from my experience.
While I had them all together on the carpet I explained to them that you had developed this puzzle problem for me by adding 3 decimal numbers vertically and I wrote what you did to create it on out whiteboard. It seemed to make sense to them. I said that they were going to create their own problems and then we were going to create “disappearing decimal puzzles” for the other 5th grade class to solve. Their were cheers of joy! Nothing like trying to stump your fellow classmates. Ha! I gave them a handout with the steps on how to create the puzzles that you listed in your blog post. I asked them to do their work on the front but when they were ready to create the puzzle to be solved they should write it horizontally on the back of the paper so they could test it out on one of their classmates. Again they enthusiastically got busy creating their puzzles. I haven’t had a chance to look them over yet but I will scan them and share them with you. We ran out of time (because we did our Decimal of the Day work first,) so we will continue our exploration tomorrow. I will update you on their progress and the results. Maybe we will even send you a few problems to solve.
Thanks, Nina, for the detailed report of what happened with your students. I like the idea of them being able to add decimal points and also zeroes. I hadn’t thought about the zeroes. Thanks again and keep me posted.
Hello again, Marilyn. Here is the rest of the story from my 5th grade classrooms. The students had great fun generating puzzles for their peers in the other class to solve. The open-ended nature of the problem allowed every student to access the puzzle creation. In the end, two of the more simple puzzles ended up being more challenging than the more complex puzzles. Here is an example created by “Mark”: 169 + 9 = 1.78. The idea of putting in a zero in the tenths place before the 9 did not occur to most of the students. When this happened they brought the card back and told me, “Mark’s card is not correct.” I assured them it was correct and that they could consult a partner or continue to work on their own. After a few minutes I heard, “AHHH, now I get it!” I love the card because it requires them to truly think about the meaning of each of the decimal place values. Another card was “Theo’s” card: 255 + 1005 = 126. He wrote it this way and several students asked if we forgot to put the decimal point in the sum. To make sure they understood he did not omit the decimal point we rewrote the sum as 126.0. Theo and Mark were proud their problems were viewed as challenging.
Another problem that I thought would not be so challenging but ended up so was “Monroe’s” problem: 357 + 357 + 357 = 39.627. At first glance it seemed to be one that would be easier to solve but I think the students were challenged by thinking about 357 as being written three different ways, 35.7, 3.57 and .357.
There were other problems considered to be challenging as well but mostly because the addends had more than 3 digits. I am glad we had different types of problems for every type of student thinking.
It was fun to watch the students solve the problems. It appeared that they looked at the sum then started to estimate in their minds what one of the addends would need to be to get close to the sum. Once they had the one addend they could pretty quickly place the decimal points in the other two addends. An excellent feature of this type of problem solving is that the answer is provided so the students have to keep working until they do get the sum. On average every student solved about 10 problems in about 50 minutes. Again, the lesson is naturally differentiated by the nature of the lesson.
Do I think my students can now add decimals? By all means and I never once had to say, “Line up the decimal points before you add.” In fact, most of the students added the problems horizontally.
Thanks, Marilyn, for another amazing lesson! I believe you mentioned this could also be used for multiplication?
Thanks for this additional comment. Hey, maybe you should think about writing a blog yourself! I’d love to hear more about your classroom. About multiplication of decimals: I think that instead of having students learn to “count the number of decimal places,” I’d rather have them estimate and put the decimal point in the place that makes sense. For example, multiplying 2.14 x 6.3 has to me a bit more than 12, so inserting the decimal point in the answer to produce 13.482 is the only possible location. For me, it’s always about making sense, not learning rules. Thanks again!
Thank you, Marilyn! I will definitely try this lesson with multiplication.
Thanks, too, for the blog recommendation. I started a blog two years ago but I have not done a good job of keeping it up. Sounds like it might be time to fire it up again.
Nina
this is awesome and so helpful.
Thank you for sharing these ideas! I’m curious if you incorporate any number line work into your teaching of these concepts?
Yes. Here’s what I wrote relating to fractions:
I can only see “Yes. Here’s what I wrote relating to fractions:” – – – Is there a link?
Oops. Here’s the Fractions on a number line link.
Oops. I forgot the link: https://marilynburnsmath.com/fractions-on-a-number-line/
This worked wonderfully in class last week. Will give the other numbers written by other teachers on the students this week. Thanks for sharing 🙂
I have made a number slider (the decimal point never moves!) and number expander (see that 18 tenths = 1.8) so that students can see the relationships of x10 and /10 etc . The template is free at tes.com under resources, just search for my name (Christine Lenghaus). They are well worth your time to make them.
https://www.youtube.com/watch?v=X55dj_oRWM4
The expander I have as a template has pictures on it but here’s an example of it being used: https://www.youtube.com/watch?v=TowrTxft7Jo
I have seen the puzzle with the three numbers before and I think it’s a great way to teach decimals!