When Is a Square Half as Big as Another Square?

I realize that using “half as big” in my question isn’t mathematically precise, but it’s how I posed the question recently to students, first to fourth graders and then to fifth graders. I wanted the students to try and visualize what two squares would look like, one centered within the other, with the area of the smaller square one-half the area of the larger square.

Before I presented the problem to students, I reached out for digital help to math friends. I had a thought that was sort of a-teacher-can-dream request. What if I projected two squares as shown below and ask a question that I thought would have an obvious answer: Is the area of the yellow square more than half, less than half, or about half of the area of the blue square?

 Next, I’d project two squares as shown below and ask the same question: Is the area of the yellow square more than half, less than half, or about half of the area of the blue square?

Then, my teaching dream was to be able to go back to the original yellow square and drag a corner so that it would increase in size while staying in position in the middle of the blue square. I would ask students to call Stop! when they estimated that the yellow square was half the size of the blue square. (The idea is similar to how I’ve asked students to estimate where numbers should be marked on a number line, when I slowly drag my finger on a line and they shout out when they think I should stop. I posted a blog about that lesson: Teaching a Number Line Lesson.)

I fiddled with PowerPoint to help me and was only able to generate separate slides.

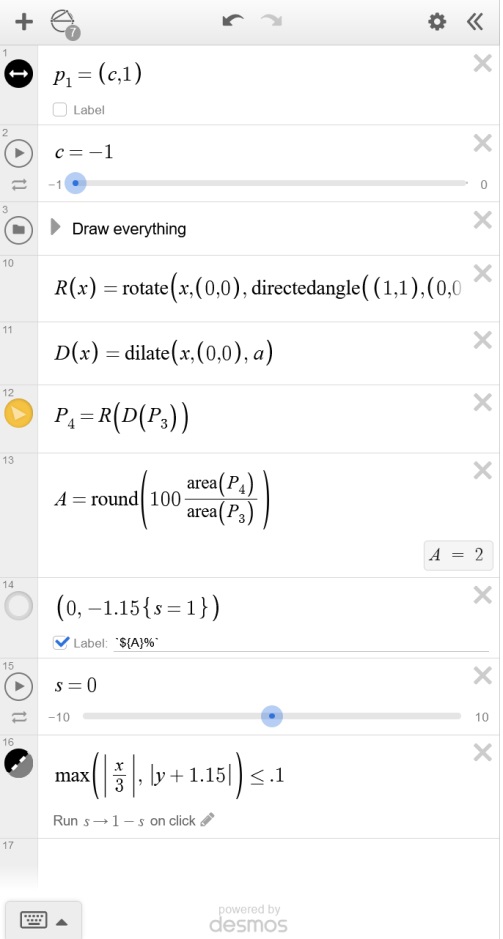
That’s when I reached out to friends. About an hour after I sent my request, I received a Desmos graph from Eli Luberoff that did just what I wanted. (Eli is the founder of Desmos  that has made an online graphing calculator free for anyone to use. From the Desmos website: At Desmos Studio we want to help everyone learn math, love math, and grow with math.)

What Eli sent me was perfect. When I dragged a corner of the yellow square, it increased in size while staying positioned in the center of the blue square.

Eli tried the tool with a group the next day and then wrote to me again, sending an enhanced version with some features that made a perfect digital tool even more perfect. He explained:
Drag the black point to change the size of the inner square.
Drag the gray point in the upper left to rotate the inner square.
Click the gray box underneath to reveal the percents.

With Eli’s permission, here’s the link so you can access the tool and explore its features. It’s wonderful. (Thank you, Eli!)

From My First Classroom Experience 
Here’s a glimpse of my first time using the tool with a class. When I projected the yellow square as shown in the photo below, it was obvious to the students that the yellow square was less than half the area of the blue square. When I enlarged the yellow square so it almost covered the blue square, it was also obvious to them that it was more than half the area. Then I reduced the yellow square to its beginning size and slowly, slowly dragged a corner until they called Stop!

What Came Next?
This experience was the introduction to a lesson about comparing areas of squares. After I introduced the Desmos tool and the students made their initial prediction, I engaged them with a sequence of experiences with milk cartons and Origami squares. Then I returned to the Desmos tool. I’m finishing up that blog now and will post soon. Stay tuned.

P.S. One student in the class asked, “How does the Desmos app work?” I showed the left panel of the tool that I had hidden from their view and said, “These are the equations that make the tool work.” I hope that seeing these served to inspire their curiosity about the power of equations.