I typically write blogs after teaching a lesson to share what I did and what I learned. This blog is different. I’m deep into planning a lesson for fourth graders about place value and number lines. It’s a lesson that I’ve never tried before with students but that I’ve been thinking about for a while.
The inspiration for the lesson is a Tweet from when Twitter was still Twitter. Mark Chubb posted it in 2016, evidence that I’ve truly been thinking about this lesson for a long while. When I first saw the Tweet, I struggled to think about where 1 billion would go. It wasn’t obvious to me.
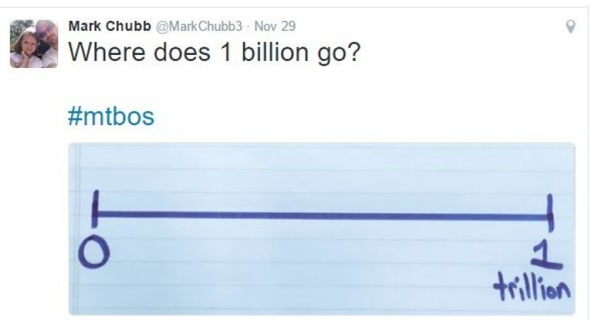
Using the Tweet in a PD Session
Shortly after seeing the Tweet, I used it as an opener in a PD session for K–5 teachers at John Muir Elementary School in San Francisco. I just searched my files and found the planning notes I had sent to Sara Liebert, who had organized the session. They’re dated December 8, 2016. Here’s what I wrote:
I won’t start with the problem Mark posed in his Tweet, but instead by having them locate points on various other numbers lines. I’ll start first, probably, with a line from 0 to 10, ask them to estimate where 7 would go, then move my finger slowly across the line from zero until they call Stop. I’ve used this technique in the classroom and kids always respond positively to the guessing part. This introduction will model for teachers how they could use simple number line problems like these with their students.
After estimating where 7 would go, I’ll erase the 10, replace it with 100, and ask them to estimate where 10 would go, using the same finger routine. (Or maybe I’ll ask them to estimate a few numbers―50, 40, 65. I’m not sure.)
Next, I’ll replace the 100 with 1000 and ask them to estimate where 100, or some other numbers, would go. And then maybe I’ll change 1000 to 1 million and ask where 1000 would go. Finally, I’ll present the problem that Mark posted. I suspect that even though I’ve scaffolded the problem, it will still be a challenge.
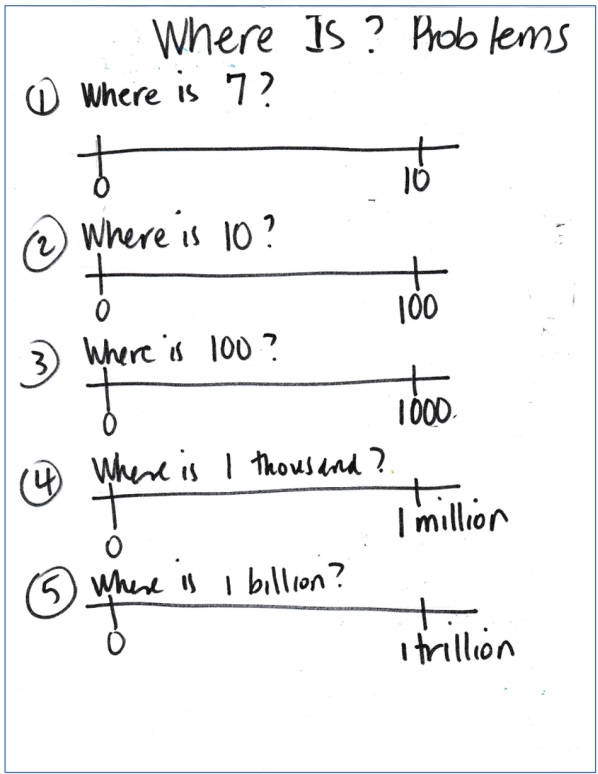
I created this outline of what I planned to do in the PD session.
Where I Am Now
So now I’m planning (finally) how to use this idea with Aimee Levin’s fourth graders at Edna Maguire School in Mill Valley. In various lessons over the years, I’ve used the routine of moving my finger across a number line and asking students to tell me when to stop. (I describe this routine in a blog I wrote in 2016, “Fractions on a Number Line.”) Now I’m thinking about using it to learn about how students would think about whole number problems.
Some of My Questions
- What problems should I use to scaffold the experience?
- Will the students be engaged in the lesson?
- What will Aimee and I learn about the students’ understanding of place value?
- Which would be difficult for them, even beyond their mathematical reach right now?
- What individual work should I ask them to do so that we would gain insights into their understanding and reasoning?
My Plan
I strive when planning lessons to be sure to begin with an experience that will be accessible to all students and then feel my way into more challenges. I always have a plan, but I’m prepared to make adjustments as I receive feedback from the students. Here’s an outline of my current plan:
- Start with locating 7 on a number line with 0 and 10 located, introducing the routine of moving my finger across and asking them to tell me when to stop.
- Move to another number line with 0 and 100 located, and ask them to locate a few numbers. I’m thinking about 50, 10, 38, and 83. (I used 38 and 83 as numbers with the digits reversed, which I’m doing to plan for a follow-up independent partner activity.)
- Next introduce another number line with 0 and 1000 located, and first have them locate the numbers I used for the 0–100 number line, but each multiplied by 10―500, 100, 380, and 830.
- Stay with this number line and ask them to locate the numbers we used with the 0–100 number line―50, 10, 38, and 83.
- Give them an individual assignment with several number lines on which they should locate numbers and an additional option if they’d like to try a challenge.
I’m Not Planning Alone
I appreciate Aimee’s willingness to let me “borrow” her class to try out an idea that I’m interested in. I met Aimee’s class once before when I taught a division lesson that I blogged about, “Mulling about Teaching Division.” I planned the division lesson with Jenna Laib, and she and I talked recently about this number line lesson that I’m going to try. We agreed that starting with problems that were accessible to all was a good idea and our conversation resulted in my plan above. I also talked with Stephanie Sheffield, with whom I’ve collaborated on various projects, and she wondered about how the fourth graders might think about the distance the numbers 38 and 83 were away from the ends of the number line, that is if 38 was about the same, farther, or closer to zero than 83 was from 100. I may also go to Muir in San Francisco and try the lesson with fourth or fifth graders there. I’ve been going to Muir since I met Sara Liebert in 2015 when she was a classroom teacher. Sara then became the school math coach, is now the principal, and we’re still collaborating.
I’ll post again after the teach the lesson to describe what occurred and offer my reflection.

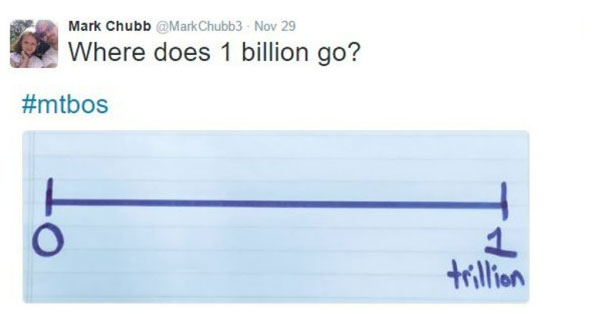
A billion is one thousandth of a trillion, so to define a billion on a number line that collates in a Trillion you would need to divide into thousands.
Yes, important for kids to learn but hard to grasp.
In your step 3, you multiply EACH number by 10 and so keep the ratios the same. Multiplying by 10 is the same as adding a zero to the end of each number. You could expand that part to add another zero, and another — seeing that the ratio [placement on the line] remains the same.
Then, logically, if you took some larger numbers and REMOVED A ZERO from the end of each, that ratio would remain the same.
So …
If you remove all the zeroes from a billion and the same # of zeroes from a trillion, you will have the ratio of 1-to-1000. That might be a useful way to help students understand how you know to divide the line into a thousand parts.
Thanks for your response and your suggestion. I believe that it’s best to approach topics like this from multiple perspectives, and yours can be part of the mix. Comprehending these large quantities is difficult. Marilyn (a beginning birder)