Comparing and Ordering Decimals

On an assessment about comparing decimals, the fifth graders were asked to circle the smallest of three numerals and explain why they made their selection. This was on Wednesday. There are 20 students in the class, and their choices split evenly, with 10 students correctly identifying 0.125 as the smallest and 10 students incorrectly identifying 0.45 as the smallest.

I planned a lesson to teach on Friday. My goal was to help cement or extend the understanding of students who answered correctly and help develop the understanding of those who had made the incorrect choice. I loved how the lesson unfolded and how the students were engaged.

Below is a step-by-step description of what I did with links to the PowerPoint I created, the two videos I showed, and the assignment that students completed at the end of class—all of the materials you need if you decide to try it. I’d love to hear, if you do. (I rarely plan lessons alone and, at the end of the blog, I describe how I came up with this lesson plan.)

The Plan
On the board, I wrote the plan for the lesson so the students had a sense of what we were going to do. This not only stimulated their curiosity, it alerted them that they would be completing an assignment before the end of class. A note: I made a change to the plan while I was teaching, switching Steps 3 and 4 so that the students watched both videos before I taught the class game. I’ll explain.

Step 1: The Power Point
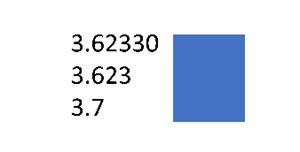
I projected this slide of the PPT and explained that I would show them numbers, revealing digits one at a time. For each slide, I’d ask the same question: Can you tell which number is greater?

I moved to the next slide and asked, “Can you tell which number is greater?” There were several responses. “They’re both the same.” “You can’t see what’s under the blue.” “Can you move the blue thing?” I responded by asking the question again, “Can you tell which number is greater? Thumbs up for yes, thumbs down for no.” All thumbs were down.

Then I showed the next four slides, repeating the question for each: Can you tell which number is greater? For each slide, I had them show thumbs up or down and then asked students to explain why they could or couldn’t tell which was greater.

I also wanted to reinforce for students how to read decimal numerals aloud, which they had been practicing. I modeled for them how to do this with these two numbers, emphasizing that we only say and for the decimal point. I pointed and read 2.06: 2 and 6 hundredths. I did the same for 2.053: 2 and 53 thousandths. Then I had them do the same in pairs. I told them, “One of you read the first numeral to your partner and then the other reads the second.”

I repeated this for four more sequences of numbers. After each I had them practice saying the numbers aloud to their partners and then had a student read each aloud for the class. The second sequence shows three numbers, so I changed my question to: Can you tell which number is greatest? (I briefly explained that we used “greater” when comparing two items and “greatest” when comparing more than two items.) For the last two sequences, I changed the question to: Can you tell which number is smaller or smallest? Below is the final slide for each sequence. (You can download the complete PPT here.)

Step 2: Showing the First Video
I reminded the class of the assignment they had completed the day before yesterday, where they decided which was smallest of 0.8, 0.45, and 0.125. I told them that they would now see a short 20-second video of me asking a fifth grader, Jacob, the same question. “Listen carefully,” I said, “and see if you can explain in your own words how Jacob reasoned.” I showed the video twice so that they would have two opportunities to hear Jacob’s thinking. And then I had about half a dozen students explain Jacob’s idea. Basically, Jacob decided by inspecting the numerals in the tenths places.

Step 3: Showing the Second Video
While I had planned to teach the class game next, I decided that giving them access to a different way of reasoning would be beneficial for when they played the game, and I selected a video of Leo Kostelnik interviewing another fifth grader. I pointed out that I was changing my plan and told them that we’d now watch another student, Eloise, answer the same question. I said, “We’ll talk afterwards how their two explanations differed.” As I did with Jacob, I showed the video of Eloise twice, and then had students explain how Eloise was thinking. Eloise reasoned by adding zeroes to 0.8 and 0.45 so that she was comparing these decimals—0.800, 0.450, and 0.125.

Step 4: Playing the Game—Put in Order
Next, I introduced the game. I had written eight decimal numerals on 4-by-6-inch index cards and held the cards fanned out, face down so they couldn’t see the numbers I had written. I said, “The game we’re going to play is called Put in Order. To start the game, someone needs to pick one of these cards.”

All hands shot up. I chose a student to select a card and used a magnet to post it on the whiteboard. (Sometimes I just set the cards on the board tray, which works well when students are gathered on the rug. But here it was easier for them to see if the numbers were posted higher up.)

I then explained, “We’re going to post all of the cards in a row on the board, in size order from the smallest to the greatest. Who would like to pick another card and put it on the board either before or after one and four hundred nineteen thousandths?” I read the posted number to continue to model for the students how to read decimal numerals.

I continued, “If you pick a card and post it, then you have to explain to the class how you decided where the number belongs. Also, if you used Jacob’s method or Eloise’s method, include that in your explanation.”

One by one, students selected and placed cards and the others indicated with hand signals whether they agreed or disagreed. For some numbers, I had multiple students explain how they reasoned. The students were involved and interested.

After all eight numbers were posted, I told them that I had one more number to place that I thought of as a special challenge. I showed them the card on which I had written 1½. There was a flurry of comments. “Hey, there’s a fraction.” “Can you do it?” “It’s tricky.” I asked them to turn and talk with their partner, and then I chose someone to place it.

“That wasn’t so hard,” a student commented. “One and a half is basically one point 5, so it had to go after the one point fours and before one point 9.”

Step 5: The Assignment
This was essentially the same as they had done two days previously with different numbers. I distributed the assignment and they got to work. (Here’s a PDF if you’d like to use it.)

Five students were absent, and of the 15 who did the assignment, all but one student correctly circled 0.278. Their explanations were a mix, some like Jacob’s, some like Eloise’s, and some a combination. Below is a sampling, with the incorrect paper at the end.

How I Created This Lesson
I exchanged emails with a few colleagues and also had a conversation with Jenna Laib, with whom I often plan lessons. As a math coach in a K–8 school, Jenna had just observed a comparing decimals lesson in a fifth-grade class. This was really fortunate for me. The teacher used a lesson from Think Math, and I adapted that lesson idea to create the PowerPoint I used. For the class game, I’ve often played Put in Order with classes using fractions, and it’s always been well received. It worked just as well here with decimals. Also, if you’re interested in learning more about interviewing students, visit Listening to Learn for information about a digital interviewing tool for students in Kindergarten and up.