Here’s a problem from the Listening to Learn (LTL) Interview 4, adding and subtracting within 100. It’s a missing number problem and, when we interview, we show students this card.

As with all of LTL interview questions, we ask students to solve the problem without paper and pencil, by reasoning in their head. How would you figure out the answer?
Two Different Ways of Reasoning
Here are video clips of how two students solved it, each getting the correct answer of 15, but each figuring out the answer in a different way. Take a look.
What I Noticed from Listening to Meeyah and Rocco
- Both arrived at the correct answer to the problem.
- Meeyah started with 90, subtracted 10, and then subtracted 5.
- Rocco knew that 100 – 75 is 25 and he subtracted 10 to get 15.
- Both Amy and Lynne were neutral listeners, allowing the students to explain their reasoning without interrupting.
How I Used These Two Listening to Learn Videos for a Class Lesson
I began with a number talk, the kind where I present one problem and have the students think about different ways to solve it mentally. I like this number sense routine for several reasons. One is that it gives me the chance to communicate directly to students that I think there’s more than one way to solve a problem. Another is that students have the opportunity to listen to and make sense of each other’s explanations. A third is that it provides a base of experience upon which I can build to introduce students to ideas that may be new for them.
This lesson did all that . . . and more.
- I wrote the problem on the board and asked students to talk with their partner (think, pair, share). This gave them time to think about how they might solve the problem and to practice explaining their reasoning. Then, as they reported, I recorded their ideas on the board. I’ve found that the process of my writing their solutions has two benefits. One is that is gives me a chance to model how to represent their thinking mathematically. Also, the process of my writing slows down the lesson and gives students time to think about their classmates’ ideas.

Here’s what the board looked like after all students who wanted to had a chance to share. No one offered Rocco’s reasoning.
- Next I showed the videos from the LTL video library. I’ve learned that it’s best to show videos like these after students had a chance to think about the problem on their own. I’ve found that this prior experience is important when I’m using videos in classroom instruction. I began with the video of Meeyah, telling them first that after they saw it, I’d ask them to talk with their partners about whether her reasoning matched an idea that I had recorded. I played the video of Meeyah twice, and the students agreed that Meeyah reasoned the way that Henry did. (That’s when I wrote “Meeyah” above Henry’s name on the board.) Amie commented that Meeyah’s method was sort of like hers since she subtracted the same numbers, 10 and 5, but in the reverse order.
- Then I showed the video of Rocco solving the same problem, also showing it twice. Since the students couldn’t find a match, I asked for their help to record Rocco’s thinking, as if he was a student in our class.

I recorded ideas from two students. After Ella described what Rocco did, Maxine commented that Rocco probably chose to start with 100 because 90 is 10 less than 100. I recorded Maxine’s idea on the board.
- To end the lesson, I gave the students a writing assignment. I asked them to write a letter to Rocco about his reasoning. I told them I was interested in how they interpreted Rocco’s explanation and also to add any other comments that they had about his thinking.

Students’ letters serve to give me feedback about what they experienced from the lesson, and also provide them the opportunity to reflect on their own thinking.
The Students’ Letters to Rocco
While it’s sometimes hard to follow someone else’s reasoning, it’s important that students learn to listen to each other’s ideas. Here’s a sampling of what they wrote.
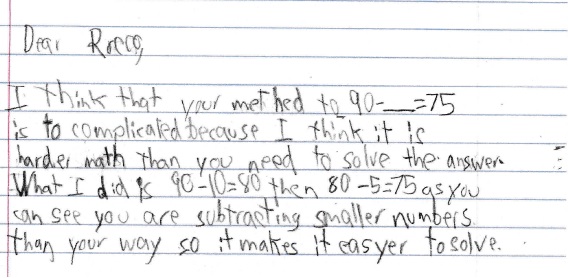
This student wrote that it was easier (for him) to subtract from 90 and that he thought Rocco’s way was too complicated.
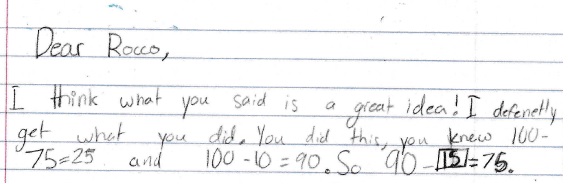
This letter expressed enthusiasm and admiration for Rocco’s idea.

This student wrote that it was hard for her to understand Rocco’s thinking, that maybe if would be simpler if he “flip the equation.” I’m still wondering what she meant by that.

In this letter, she restated Rocco’s approach and then complimented Rocco on his using 100 to reason.

This student wrote that it was hard for her to understand Rocco’s thinking, that maybe if would be simpler if he “flip the equation.” I’m still wondering what she meant by that.
My Takeaway from This Experience
When developing Listening to Learn, we listened to hundreds of students solve this problem and heard a range of explanations, similar to the ones that the students in this class offered during the number talk. Rocco’s explanation was typical in that he started with something he knew, 100 – 75, but it was unusual because we found that fewer students use 25 and multiples of 25 as benchmarks to help them reason. We’re not sure why. Maybe we just haven’t emphasized this in instruction? Maybe students today have less experience with using money and thinking about quarters? What remains most important is that we listen carefully to students, not for what we might hope to hear, but to understand how they are reasoning, and then to use what we learn to support students during instruction.

